【题目】(本题满分10分)抛物线![]() 与x轴交与
与x轴交与![]() ,
,![]() 两点,
两点,

(1)求该抛物线的解析式;
(2)设(1)中的抛物线与y轴交于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)y=-x2-2x+3;(2)存在Q(-1,2).
【解析】试题分析:(1)把A(1,0)B(-3,0)代入![]() 然后解方程组即可;(2)因为线段AC的长固定不变,所以当AQ+CQ的长最小时△QAC的周长最小,根据轴对称的性质可知直线BC与对称轴的交点即为Q点,用待定系数法求直线BC解析式,把对称轴x=-1代入即可.
然后解方程组即可;(2)因为线段AC的长固定不变,所以当AQ+CQ的长最小时△QAC的周长最小,根据轴对称的性质可知直线BC与对称轴的交点即为Q点,用待定系数法求直线BC解析式,把对称轴x=-1代入即可.
试题解析:解(1)把A(1,0)B(-3,0)代入到
![]() 3分
3分
∴抛物线的解析式为y=-x2-2x+3 5分
(2)存在。 6分
过B、C作直线BC与对称轴x=-1的交点就是Q点,
设直线BC解析式为y=kx+b,把B(-3,0)C(0,3)代入到
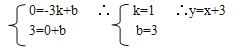
令XQ="-1" 得YQ=2 ∴Q(-1,2) 10分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,直线在平面直角坐标系中与y轴交于点A,点B(﹣3,3)也在直线上,将点B先向右平移1个单位长度,再向下平移2个单位长度得到点C,点C也在直线上.求点A的坐标和直线的解析式;
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式3ab2-2ab-1的次数为。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知多项式-m3n2-2中,含字母的项的系数为a , 多项式的次数为b , 常数项为c , 则a+b+c=
。 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(-b)4·(-b)3·(-b)5=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段AB,C是线段AB上一点,M是AB的中点,N是AC的中点.
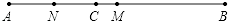
(1)若AB=8cm,AC=3.2cm,求线段MN的长;
(2)若BC=a,试用含a的式子表示线段MN的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算(x3)2的结果是( )
A.x5
B.x6
C.x8
D.x9
相关试题

