【题目】关于x的一元函数y=﹣2x+m和反比例函数y= ![]() 的图象都经过点A(﹣2,1).
的图象都经过点A(﹣2,1).
(1)求一次函数和反比例函数的解析式;
(2)求一次函数与反比例函数的另一个交点B的坐标;
(3)求△AOB的面积.
参考答案:
【答案】
(1)
解:把A(﹣2,1)代入函数关系式得到m=﹣3,n=﹣3
∴一次函数的解析式为y=﹣2x﹣3,反比例函数的解析式为y=﹣ ![]()
(2)
解:解方程组  ,得:
,得: ![]() ,
,  ,
,
∴B的坐标为( ![]() ,﹣4)
,﹣4)
(3)
解:∵一次函数的解析式为y=﹣2x﹣3,
∴y=0时,x=﹣ ![]() ,则CO=
,则CO= ![]() ,
,
∴S△AOB=S△AOC+S△BOC= ![]() =
= ![]() .
.

【解析】(1)把A的坐标代入两个函数的解析式中就可以确定两个函数的解析式;(2)利用两个函数的解析式组成方程组,然后解方程组就可以确定另一个交点的坐标;(3)先确定直线与x轴的交点C的坐标,然后用面积的割补法求△AOB的面积.
【考点精析】本题主要考查了一次函数的概念和一次函数的图象和性质的相关知识点,需要掌握一般地,如果y=kx+b(k,b是常数,k不等于0),那么y叫做x的一次函数;一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=Rt∠,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
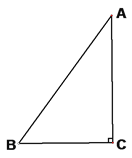
(1)出发2秒后,求△ABP的周长.
(2)问t满足什么条件时,△BCP为直角三角形?
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①abc>0;②﹣b<a+c;③4a+2b+c>0;④b2﹣4ac>0;其中正确的结论有( )
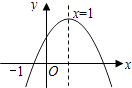
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1)x2﹣4x+1=0
(2)3(x﹣2)2=x(x﹣2). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在∠AOB的两边截取OA=OB,OC=OD,连接AD,BC交于点P,则下列结论中①△AOD≌△BOC,②△APC≌△BPD,③点P在∠AOB的平分线上。 正确的是 (填序号)
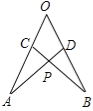
-
科目: 来源: 题型:
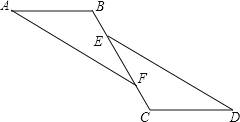
查看答案和解析>>【题目】如图,已知:点B、E、F、C在同一直线上,∠A=∠D,BE=CF,且AB∥CD.求证:AF∥ED
证明:∵BE=FC
∴BE+EF=FC+EF(____________________________)
即:___________
∵AB∥CD
∴∠B=∠C(_________________________)
在△ABF和△DCE中,
∠A=∠D, ∠B=∠C, BF=CE
∴△ABF≌△DCE(________)
∴∠AFB=∠DEC(_________________________________)
∴AF∥ED(__________________________________)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y=y1﹣y2 , y1与x2成正比例,y2与x﹣1成反比例,当x=﹣1时,y=3;当x=2时,y=﹣3.
(1)求y与x之间的函数关系;
(2)当x=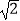 时,求y的值.
时,求y的值.
相关试题

