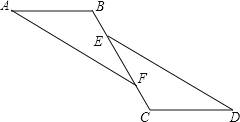
【题目】如图,已知:点B、E、F、C在同一直线上,∠A=∠D,BE=CF,且AB∥CD.求证:AF∥ED
证明:∵BE=FC
∴BE+EF=FC+EF(____________________________)
即:___________
∵AB∥CD
∴∠B=∠C(_________________________)
在△ABF和△DCE中,
∠A=∠D, ∠B=∠C, BF=CE
∴△ABF≌△DCE(________)
∴∠AFB=∠DEC(_________________________________)
∴AF∥ED(__________________________________)
参考答案:
【答案】等式的性质BF=CE两直线平行内错角相等AAS全等三角形对应角相等内错角相等两直线平行
【解析】
由BE= CF,利用等式的性质得到BF= CE ,再由AB与DC平行得到两对内错角相等,利用AAS得到△ABF与△DCE全等,利用全等三角形的对应角相等得到一对内错角相等,利用内错角相等两直线平行即可得证.
证明:∵BE=FC
∴BE+EF=FC+EF( 等式的性质 )
即: BF=CE
∵AB∥CD
∴∠B=∠C( 两直线平行内错角相等 )
∠A=∠D
∠B=∠C
在△ABF和△DCE中,有
BF=CE
∴△ABF≌△DCE( AAS )
∴∠AFB=∠DEC( 全等三角形对应角相等 )
∴AF∥ED( 内错角相等两直线平行 )
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1)x2﹣4x+1=0
(2)3(x﹣2)2=x(x﹣2). -
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元函数y=﹣2x+m和反比例函数y=
 的图象都经过点A(﹣2,1).
的图象都经过点A(﹣2,1).
(1)求一次函数和反比例函数的解析式;
(2)求一次函数与反比例函数的另一个交点B的坐标;
(3)求△AOB的面积. -
科目: 来源: 题型:
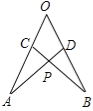
查看答案和解析>>【题目】如图:在∠AOB的两边截取OA=OB,OC=OD,连接AD,BC交于点P,则下列结论中①△AOD≌△BOC,②△APC≌△BPD,③点P在∠AOB的平分线上。 正确的是 (填序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y=y1﹣y2 , y1与x2成正比例,y2与x﹣1成反比例,当x=﹣1时,y=3;当x=2时,y=﹣3.
(1)求y与x之间的函数关系;
(2)当x=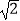 时,求y的值.
时,求y的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长度为1个单位长度的小正方形组成的正方形中,点A、B、C在小正方形的顶点上.
 在图中画出与
在图中画出与 关于直线l成轴对称的
关于直线l成轴对称的 ;
; 三角形ABC的面积为______;
三角形ABC的面积为______; 以AC为边作与
以AC为边作与 全等的三角形,则可作出______个三角形与
全等的三角形,则可作出______个三角形与 全等;
全等;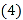 在直线l上找一点P,使
在直线l上找一点P,使 的长最短.
的长最短.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB边的垂直平分线
 交BC于D,AC边的垂直平分线
交BC于D,AC边的垂直平分线 交BC于E,
交BC于E, 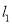 与
与 相交于点O,△ADE的周长为6cm.
相交于点O,△ADE的周长为6cm.(1)求BC的长;
(2)分别连结OA、OB、OC,若△OBC的周长为16cm,求OA的长;

相关试题

