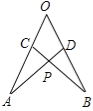
【题目】如图:在∠AOB的两边截取OA=OB,OC=OD,连接AD,BC交于点P,则下列结论中①△AOD≌△BOC,②△APC≌△BPD,③点P在∠AOB的平分线上。 正确的是 (填序号)
参考答案:
【答案】①②③
【解析】
试题分析:根据题中条件,由两边夹一角可得△AOD≌△BOC,得出对应角相等,又由已知得出AC=BD,可得△APC≌△BPD,同理连接OP,可证△AOP≌△BOP,进而可得出结论.
∵OA=OB,OC=OD,∠O为公共角,
∴△AOD≌△BOC,
∴∠A=∠B,
又∠APC=∠BPD,
∴∠ACP=∠BDP,
OA-OC=OB-OD,即AC=BD,
∴△APC≌△BPD,
∴AP=BP,
连接OP,
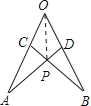
即可得△AOP≌△BOP,得出∠AOP=∠BOP,
∴点P在∠AOB的平分线上.
故题中结论都正确.
故答案为:①②③.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )
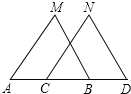
A.∠M=∠N B.AM=CN C.AB=CD D.AM∥CN
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的二次方程(m+1)x2+5x+m2-3m=4的常数项为0,则m的值为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题提出:用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
问题探究:不妨假设能搭成
 种不同的等腰三角形,为探究
种不同的等腰三角形,为探究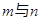 之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.探究一:
(1)用3根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
此时,显然能搭成一种等腰三角形。所以,当
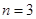 时,
时,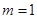
(2)用4根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
只可分成1根木棒、1根木棒和2根木棒这一种情况,不能搭成三角形
所以,当
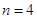 时,
时,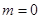
(3)用5根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和3根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和1根木棒,则能搭成一种等腰三角形
所以,当
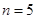 时,
时,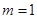
(4)用6根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和4根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和2根木棒,则能搭成一种等腰三角形
所以,当
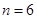 时,
时,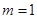
综上所述,可得表①
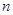
3
4]
5
6
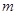
1
0
1
1
探究二:
(1)用7根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?
(仿照上述探究方法,写出解答过程,并把结果填在表②中)
(2)分别用8根、9根、10根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三
角形?(只需把结果填在表②中)
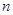
7
8
9
10
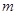
你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究,……
解决问题:用
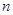 根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?(设
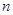 分别等于
分别等于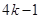 、
、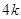 、
、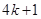 、
、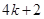 ,其中
,其中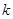 是整数,把结果填在表③中)
是整数,把结果填在表③中)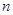
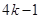
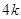
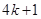
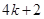
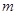
问题应用:用2016根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?(要求写出解答过程)其中面积最大的等腰三角形每个腰用了__________________根木棒。(只填结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】两三角形的相似比为1∶4,它们的周长之差为27 cm,则较小三角形的周长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AD=2AB=4,E是AD的中点,一块足够大的三角板的直角顶点与点E重合,将三角板绕点E旋转,三角板的两直角边分别交AB,BC(或它们的延长线)于点M,N,设∠AEM=α(0°<α<90°),给出下列四个结论:
①AM=CN;②∠AME=∠BNE;③BN﹣AM=2;④S△EMN=
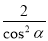 .
.上述结论中正确的个数是( )
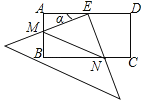
A.1 B.2 C.3 D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种花卉每盆的盈利与每盆的株数有一定的关系,每盆植3株时,平均每株盈利4元;若每盆增加1株,平均每株盈利减少0.5元,要使每盆的盈利达到15元,每盆应多植多少株?设每盆多植x株,则可以列出的方程是( )
A.(3+x)(4-0.5x)=15B.(x+3)(4+0.5x)=15
C.(x+4)(3-0.5x)=15D.(x+1)(4-0.5x)=15
相关试题

