【题目】如图，AC⊥BC，DC⊥EC，AC=BC,DC=EC,若AC=3，CE=4，则AD2+BE2=__________．
【答案】50
【解析】
由△ACE≌△BCD（SAS），推出AE⊥BD，再利用勾股定理即可解决问题．
解：设AC交BD于点J．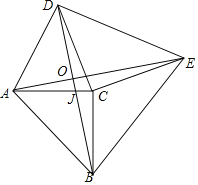
∵AC⊥BC，DC⊥EC，
∴∠ACB=∠DCE=90°，
∴∠ACE=∠DCB，
∵AC=BC，DC=EC，
∴△ACE≌△BCD（SAS），
∴∠CAE=∠CBD，
∵∠CBJ+∠BJC=90°，∠BJC=∠AJO，
∴∠JAO+∠AJO=90°，
∴∠AOJ=90°，
∴AE⊥BD，
∵AC=3，EC=4，
∴AB2=32+32=18，DE2=CD2+CE2=32，
∴AD2+BE2=OD2+OA2+OE2+OB2=（OD2+OE2）+（OA2+OB2）=18+32=50．
故答案为：50．
科目：初中数学 来源： 题型：
【题目】节能又环保的油电混合动力汽车，既可以用油做动力行驶，也可以用电做动力行驶，某品牌油电混合动力汽车从甲地行驶到乙地，若完全用油做动力行驶，则费用为80元；若完全用电做动力行驶，则费用为30元，已知汽车行驶中每千米用油费用比用电费用多0.5元．
(1)求：汽车行驶中每千米用电费用是多少元？甲、乙两地的距离是多少千米？
(2)若汽车从甲地到乙地采用油电混合动力行驶，且所需费用不超过50元，则至少需要用电行驶多少千米？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB＝AC，过点B作BD⊥AC，垂足为D，若D是边AC的中点，
（1）求证：△ABC是等边三角形；
（2）在线段BD上求作点E，使得CE＝2DE（要求：尺规作图，不写画法，保留作图痕迹）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一次函数y1=﹣x+5的图象与反比例函数y2=
（k≠0）在第一象限的图象交于A（1，n）和B两点．
（1）求反比例函数的解析式；
（2）当y2＞y1＞0时，写出自变量x的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】二次函数
，
，
是常数，且
中的
与
的部分对应值如下表所示，则下列结论中，正确的个数有（ ）
|
|
|
|
|
|
|
|
|
|
；
当
时，
；
当
时，的值随值的增大而减小；
方程
有两个不相等的实数根．
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在日历上我们可以发现其中某些数满足一定的规律.如图是2018年8月份的日历，我们任意选择其中所示的方框部分，将方框部分中的4个位置的数交叉相乘，再相减，如8×16－9×15=－7,19×27－20×26=－7，不难发现结果都是－7.
（1）请你再选择一组数按上面的方式计算，看看是否符合这个规律.并用你擅长的表达方式描述这个规律.
（2）请你利用整式的运算对以上的规律加以证明.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：在四边形ABCD中，E，F分别是AB，AD边上的点，DE与CF相交于点G.
(1)如图①，若四边形ABCD是矩形，且DE⊥CF.求证：
；
(2)如图②，若四边形ABCD是平行四边形，试探究：当∠B与∠EGC满足什么关系时，成立？并证明你的结论；
(3)如图③，若BA＝BC＝9，DA＝DC＝12，∠BAD＝90°，DE⊥CF.求
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下面是课本中“作一个角等于已知角”的尺规作图过程．已知：∠AOB． 求作：一个角，使它等于∠AOB．作法：如图
（1）作射线O'A'；
（2）以O为圆心，任意长为半径作弧，交OA于C，交OB于D；
（3）以O'为圆心，OC为半径作弧C'E'，交O'A'于C'；
（4）以C'为圆心，CD为半径作弧，交弧C'E'于D'；
（5）过点D'作射线O'B'．
则∠A'O'B'就是所求作的角．
请回答：该作图的依据是（ ）
A.SSSB.SASC.ASAD.AAS
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
