【题目】(12分)如图,在正方形ABCD中,E是AD的中点,F是BA延长线上的一点,AF=AB,已知△ABE≌△ADF.
(1)在图中,可以通过平移、翻折、旋转中的哪一种方法,使△ABE变到△ADF的位置;
(2)线段BE与DF有什么关系?证明你的结论.

参考答案:
【答案】(1)见解析;
【解析】试题分析:(1)利用正方形的性质得到∠BAD=90°,而△ABE≌△ADF,则利用旋转的定义可将△ABE绕点A逆时针旋转90°可得到△ADF;
(2)利用全等三角形的性质可得BE=DF,ABE=∠ADF,则利用对顶角相等和三角形内角和可判断∠DHE=∠EAB=90°,从而得到BE⊥DF.
试题解析:(1)把△ABE绕点A逆时针旋转90°可得到△ADF;
(2)BE=DF,BE⊥DF.理由如下:
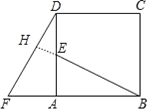
∵△ABE≌△ADF,
∴BE=DF,∠ABE=∠ADF,
而∠AEB=∠DEH,
∴∠DHE=∠EAB=90°,
∴BE⊥DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于x的方程:mx2﹣(3m﹣1)x+2m﹣2=0.
(1)求证:无论m取何值时,方程恒有实数根;
(2)若关于x的二次函数y=mx2﹣(3m﹣1)x+2m﹣2的图象与x轴两交点间的距离为2时,求抛物线的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,AD是弦,∠A=22.5°,延长AB到点C,使得∠ACD=45°.
(1)求证:CD是⊙O的切线.
(2)若AB=2
 ,求OC的长.
,求OC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(﹣2x)2的结果是( )
A.2x2B.﹣2x2C.4x2D.﹣4x2
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某校初三400名学生的体重情况,从中抽取50名学生的体重进行分析.在这项调查中,下列说法正确的是( )
A.400名学生中每位学生是个体
B.400名学生是总体
C.被抽取的50名学生是总体的一个样本
D.样本的容量是50
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,四边形OABC四个顶点的坐标分别为O(0,0),A(﹣3,0),B(﹣4,2),C(﹣1,2).将四边形OABC绕点O顺时针旋转90°后,点A、B、C分别落在点A′、B′、C′处.
(1)请你在所给的直角坐标系中画出旋转后的四边形OA′B′C′;
(2)点C旋转到点C′所经过的弧的半径是 ,点C经过的路线长是 .

-
科目: 来源: 题型:
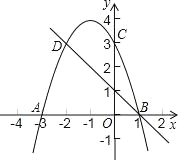
查看答案和解析>>【题目】如图,二次函数y1=ax2+bx+3的图象与x轴相交于点A(﹣3,0)、B(1,0),交y轴于点C,C、D是二次函数图象上的一对对称点,一次函数y2=mx+n的图象经过B、D两点.
(1)求二次函数的解析式及点D的坐标;
(2)根据图象写出y2>y1时,x的取值范围.
相关试题

