【题目】如图是无盖长方体盒子的表面展开图.
(1)求表面展开图的周长(粗实线的长);
(2)求盒子底面的面积.
参考答案:
【答案】解:(1)如图所示:表面展开图的周长为:2a+2b+4c;
(2)盒子的底面长为:a﹣(b﹣c)=a﹣b+c.
盒子底面的宽为:b﹣c.
盒子底面的面积为:(a﹣b+c)(b﹣c)=ab﹣b2+2bc﹣ac﹣c2
【解析】(1)该几何体的周长是图中粗实线的长度:根据矩形的性质进行答题;
(2)根据图示求得盒子的长与宽,然后根据矩形的面积公式进行解答.
【考点精析】根据题目的已知条件,利用几何体的展开图的相关知识可以得到问题的答案,需要掌握沿多面体的棱将多面体剪开成平面图形,若干个平面图形也可以围成一个多面体;同一个多面体沿不同的棱剪开,得到的平面展开图是不一样的,就是说:同一个立体图形可以有多种不同的展开图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】回答下列问题:
(1)如图所示的甲、乙两个平面图形能折什么几何体?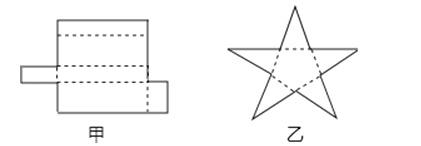
(2)由多个平面围成的几何体叫做多面体.若一个多面体的面数为f,顶点个数为v,棱数为e,分别计算第(1)题中两个多面体的f+v﹣e的值?你发现什么规律?
(3)应用上述规律解决问题:一个多面体的顶点数比面数大8,且有50条棱,求这个几何体的面数. -
科目: 来源: 题型:
查看答案和解析>>【题目】直线 y=kx+b 与直线
 交点的纵坐标为 5,而与直线 y=3x﹣9 的交点的横 坐标也是 5,则直线 y=kx+b 与两坐标轴围成的三角形面积为( )
交点的纵坐标为 5,而与直线 y=3x﹣9 的交点的横 坐标也是 5,则直线 y=kx+b 与两坐标轴围成的三角形面积为( )A.
 B.
B.  C. 1 D.
C. 1 D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】王老师自驾轿车沿高速公路从A地到B地旅游,途经两座跨海大桥,共用了4.5小时;返回时平均速度提高了10千米/小时,比去时少用了半小时回到A地.
(1)求A、B两地间的路程.
(2)两座跨海大桥的长度及过桥费见表.

该省交通部门规定:轿车的高速公路通行费y(元)的计算方法为:y=ax+b+5,其中a(元/千米)为高速公路里程费,x(千米)为高速公路里程(不包括跨海大桥长),b(元)为跨海大桥过桥费.若王老师从A地到B地所花的高速公路通行费为295.4元,求轿车的高速公路里程费a.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)观察发现
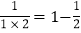 ,
,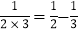 ,
,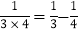 ,……,
,……,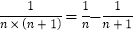 .
. =1﹣
=1﹣ =
= .
.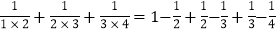 =1﹣
=1﹣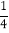 =
=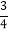 .
.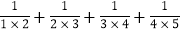 = .
= .(2)构建模型
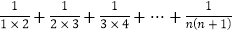 = .(n为正整数)
= .(n为正整数)(3)拓展应用:
①
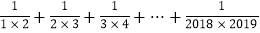 = .
= .②
 = .
= .③一个数的八分之一,二十四分之一,四十八分之一,八十分之一的和比这个数的四分之一小1,求这个数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O(0,0),A(0,1)是正方形OAA1B的两个顶点,以OA1对角线为边作正方形OA1A2B1 , 再以正方形的对角线OA2作正方形OA1A2B1 , …,依此规律,则点A2017的坐标是( )
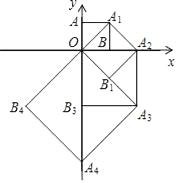
A.(0,21008)
B.( ,
,  )
)
C.(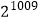 ,0)
,0)
D.(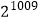 ,-
,- 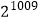 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某花园护栏是用直径为
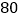 厘米的半圆形条钢组制而成,且每增加一个半圆形条钢,护栏长度就增加
厘米的半圆形条钢组制而成,且每增加一个半圆形条钢,护栏长度就增加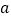 厘米
厘米 .设半圆形条钢的总个数为
.设半圆形条钢的总个数为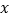 (
(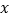 为正整数),护栏总长度为
为正整数),护栏总长度为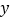 厘米.
厘米. (1)当
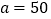 ,
,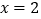 时,护栏总长度
时,护栏总长度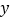 为________厘米;
为________厘米;(2)当
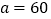 时,用含
时,用含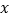 的代数式表示护栏总长度
的代数式表示护栏总长度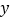 (结果要化简);
(结果要化简);(3)在第(2)题的条件下,若要使护栏总长度保持不变,而把
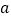 改为50
改为50 ,就要共用
,就要共用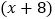 个半圆形条钢,请求出
个半圆形条钢,请求出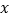 的值.
的值.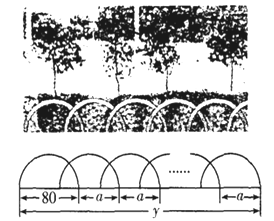
相关试题

