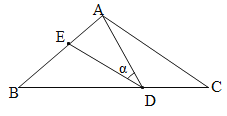
【题目】如图,在△ABC中,AB=AC=15,点D是BC边上的一动点(不与B、C重合),∠ADE=∠B=∠α,DE交AB于点E,且tan∠α=![]() .有以下的结论:①△ADE∽△ACD;②当CD=9时,△ACD与△DBE全等;③△BDE为直角三角形时,BD为12或
.有以下的结论:①△ADE∽△ACD;②当CD=9时,△ACD与△DBE全等;③△BDE为直角三角形时,BD为12或![]() ;④0<BE≤
;④0<BE≤![]() ,其中正确的结论是 (填入正确结论的序号).
,其中正确的结论是 (填入正确结论的序号).
参考答案:
【答案】②③.
【解析】
试题分析:∵∠ADE=∠B=∠α,∠EAD=∠EAD,∴△ADE∽△ABD,而△ABD不一定相似△ACD,故①不正确;
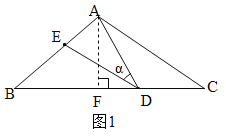
过A作AF⊥BC于F,如图1,∵AB=AC,∴BF=FC,∵tan∠α=![]() ,∠B=∠α,∴tanB=
,∠B=∠α,∴tanB=![]() ,∴cosB=
,∴cosB=![]() ,∴
,∴![]() ,∴BF=
,∴BF=![]() AB=12,∴BC=24,∵DC=9,∴BD=BC-DC=15,∴BD=AC,∵AB=AC,∴∠B=∠C,∴∠α=∠C,∵∠C+∠CAD=∠α+∠BDE,∴∠BDE=∠CAD,在△BED和△CDA中,∵∠BDE=∠CAD,BD=AC,∠B=∠C,∴△BDE≌△CAD,故②正确;
AB=12,∴BC=24,∵DC=9,∴BD=BC-DC=15,∴BD=AC,∵AB=AC,∴∠B=∠C,∴∠α=∠C,∵∠C+∠CAD=∠α+∠BDE,∴∠BDE=∠CAD,在△BED和△CDA中,∵∠BDE=∠CAD,BD=AC,∠B=∠C,∴△BDE≌△CAD,故②正确;
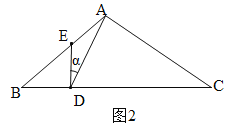
若△BDE为直角三角形,则有两种情况:(1)若∠BED=90°,∵∠BDE=∠CAD,∠B=∠C,∴△BDE∽△CAD,∴∠CDA=∠BED=90°,∴AD⊥BC,∵AB=AC,∴BD=![]() BC=12;
BC=12;
(2)若∠BDE=90°,如图2,设BD=x,则DC=24-x,∵∠CAD=∠BDE=90°,∠B=∠C=∠α,∴cos∠C=cosB=![]() ,∴
,∴![]() ,解得:
,解得:![]() ,∴若△BDE为直角三角形,则BD为12或
,∴若△BDE为直角三角形,则BD为12或![]() ,故③正确;
,故③正确;
设BE=x,CD=y,∵△BDE∽△CAD,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,∴0<BE≤
,∴0<BE≤![]() ,∴故④错误;
,∴故④错误;
故答案为:②③.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,把一张长方形的纸片ABCD沿对角线BD折叠,点C落在E处,BE交AD于点F.

(1)求证:FB=FD;
(2)如图2,连接AE,求证:AE∥BD;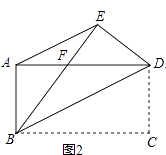
(3)如图3,延长BA,DE相交于点G,连接GF并延长交BD于点H,求证:GH垂直平分BD.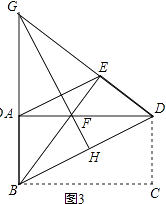
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )
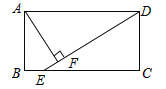
A.△AFD≌△DCE B.AF=
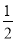 AD C.AB=AF D.BE=AD﹣DF
AD C.AB=AF D.BE=AD﹣DF -
科目: 来源: 题型:
查看答案和解析>>【题目】2010年3月份,某市市区一周空气质量报告中某项污染指数的数据是:31,35,31,34,30,32,31,这组数据的中位数、众数分别是( )
A.32,31
B.31,32
C.31,31
D.32,35 -
科目: 来源: 题型:
查看答案和解析>>【题目】若x、y互为倒数,则(-xy) 2018=_________;
-
科目: 来源: 题型:
查看答案和解析>>【题目】若ab=3,a﹣4b=5,则a2b﹣4ab2的值是 .
-
科目: 来源: 题型:
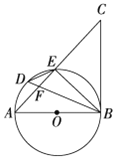
查看答案和解析>>【题目】如图,AB是⊙O的直径,点D是弧AE上一点,且∠BDE=∠CBE,BD与AE交于点F.
(1)求证:BC是⊙O的切线;
(2)若BD平分∠ABE,求证:DE2=DF·DB;
(3)在(2)的条件下,延长ED,BA交于点P,若PA=AO,DE=2,求PD的长.
相关试题

