【题目】如图,⊙O是△ABC的内切圆,切点分别为D、E、F,∠A=80°,点P为⊙O上任意一点(不与E、F重合),则∠EPF= . 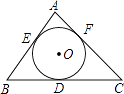
参考答案:
【答案】50°或130°
【解析】解:有两种情况: ①当P在弧EDF上时,∠EPF=∠ENF,
连接OE、OF,
∵圆O是△ABC的内切圆,
∴OE⊥AB,OF⊥AC,
∴∠AEO=∠AFO=90°,
∵∠A=80°,
∴∠EOF=360°﹣∠AEO﹣∠AFO﹣∠A=100°,
∴∠ENF=∠EPF= ![]() ∠EOF=50°,
∠EOF=50°,
②当P在弧EMF上时,∠EPF=∠EMF,
∠FPE=∠FME=180°﹣50°=130°,
所以答案是:50°或130°.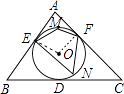
【考点精析】本题主要考查了垂线的性质和多边形内角与外角的相关知识点,需要掌握垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短;多边形的内角和定理:n边形的内角和等于(n-2)180°.多边形的外角和定理:任意多边形的外角和等于360°才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】麒麟区第七中学现有一块空地ABCD如图所示,现计划在空地上种草皮,经测量,∠B=90°,AB=3m,BC=4m,CD=13m,AD=12m.

(1)求出空地ABCD的面积?
(2)若每种植1平方米草皮需要300元,问总共需投入多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(0,2),△AOB为等边三角形,P是x轴上一个动点(不与原O重合),以线段AP为一边在其右侧作等边三角形△APQ.

(1)求点B的坐标;
(2)在点P的运动过程中,∠ABQ的大小是否发生改变?如不改变,求出其大小;如改变,请说明理由.
(3)连接OQ,当OQ∥AB时,求P点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与反比例函数y=
 的图象交于点A(﹣2,﹣5 ),C (5,n),交y轴于点B,交x轴于点D,那么不等式kx+b﹣
的图象交于点A(﹣2,﹣5 ),C (5,n),交y轴于点B,交x轴于点D,那么不等式kx+b﹣  >0的解集是 .
>0的解集是 . 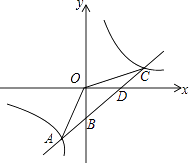
-
科目: 来源: 题型:
查看答案和解析>>【题目】乘法公式的探究及应用:

(1)如图,可以求出阴影部分的面积是_____(写成两数平方差的形式);
(2)如图,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是_____,长是_____,面积是________(写成多项式乘法的形式);
(3)比较左、右两图的阴影部分面积,可以得到乘法公式:_________(用式子表达);
(4)运用你所得到的公式,计算下列式子:(2m+n﹣p)(2m﹣n+p)
相关试题

