【题目】已知:如图,抛物线y=-x2+bx+c与x轴负半轴交于点A,与x轴正半轴交于点B,与y轴正半轴交于点C,OA=3,OB=1,点M为点A关于y轴的对称点.
(1)求抛物线的解析式;
(2)点P为第三象限抛物线上一点,连接PM、PA,设点P的横坐标为t,△PAM的面积为S,求S与t的函数关系式;
(3)在(2)的条件下,PM交y轴于点N,过点A作PM的垂线交过点C与x轴平行的直线于点G,若ON∶CG=1∶4,求点P的坐标.



参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)P(
;(3)P(![]() ,
, ![]() )
)
【解析】试题分析: ![]() 把点
把点![]() 点
点![]() 代入函数解析式
代入函数解析式![]() ,求得函数解析式即可.
,求得函数解析式即可.
![]() 点
点![]() 的横坐标为
的横坐标为![]() ,纵坐标为
,纵坐标为![]() ,利用三角形的面积公式即可表示出
,利用三角形的面积公式即可表示出![]() 的面积.
的面积.
![]() 设
设![]()
![]()
![]() 直线
直线![]() 的斜率
的斜率![]()
直线![]() 的斜率
的斜率![]() 直线
直线![]() 垂直,
垂直, ![]() 解得:
解得: ![]() 直线
直线![]() 的方程是:
的方程是: ![]() 和抛物线的方程联立,即可求出点
和抛物线的方程联立,即可求出点的坐标.
试题解析: ![]()
![]()
![]()
把![]()
![]() 代入
代入![]() ,
,
![]()
解得: ![]()
抛物线的解析式为![]()
![]() 由题意可知,点
由题意可知,点![]() ,点
,点![]()
如图所示,

![]()
点![]() 在第三象限,
在第三象限, ![]()
![]()
![]() 如图所示,
如图所示,

设![]()
![]()
![]()
直线![]() 的斜率
的斜率![]()
直线![]() 的斜率
的斜率![]()
直线![]() 垂直,
垂直, ![]()
解得: ![]()
直线![]() 的方程是:
的方程是: ![]()
联立方程: 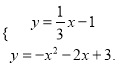
解得: 
点![]() 的坐标为:
的坐标为: 
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学校组织的社会实践活动中,甲、乙两人参加了射击比赛,每人射击七次,命中的环数如表:
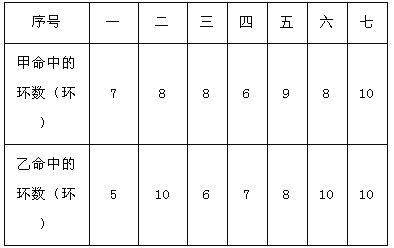
根据以上信息,解决以下问题:
(1)写出甲、乙两人命中环数的众数;
(2)已知通过计算器求得
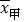 =8,
=8,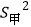 ≈1.43,试比较甲、乙两人谁的成绩更稳定?
≈1.43,试比较甲、乙两人谁的成绩更稳定? -
科目: 来源: 题型:
查看答案和解析>>【题目】下面是反映世界人口情况的数据:1957年、1974年、1987年、1999年的世界人口数依次为30亿、40亿、50亿、60亿,预计2050年世界人口将达90亿.上面的数据不能制成( )
A. 统计表B. 条形统计图
C. 折线统计图D. 扇形统计图
-
科目: 来源: 题型:
查看答案和解析>>【题目】要从甲.乙两名同学中选出一名,代表班级参加射击比赛,如图是两人最近10次射击训练成绩的折线统计图.
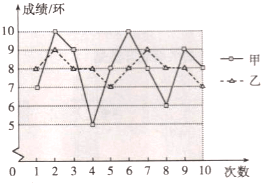
(1)已求得甲的平均成绩为8环,求乙的平均成绩;
(2)观察图形,直接写出甲,乙这10次射击成绩的方差
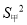 ,
, 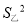 哪个大;
哪个大;(3)如果其他班级参赛选手的射击成绩都在7环左右,本班应该选 参赛更合适;如果其他班级参赛选手的射击成绩都在9环左右,本班应该选 参赛更合适.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 的
的 与
与 的部分对应值如下表:
的部分对应值如下表:
…

0
1
3
…

…

1
3
1
…
则下列判断中正确的是( )
A. 拋物线开口向上 B. 拋物线与
 轴交于负半轴
轴交于负半轴C. 当
 时,
时, D. 方程
D. 方程 的正根在3与4之间
的正根在3与4之间 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人在5次打靶测试中命中的环数如下:
甲:8,8,8,8,9
乙:5,9,7,10,9
(1)填写下表
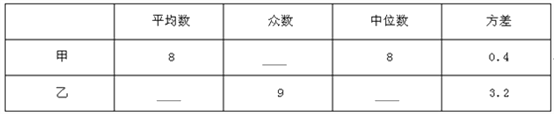
(2)教练根据5次成绩,选择甲参加射击比赛,教练的理由是什么?
(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差
(填“变大”“变小”或“不变”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】只用两枚钉子就把一根木条固定在墙上,下列语句能解释这个原理的是( )
A.木条是直的
B.两点确定一线
C.过一点可以画出无数条直线
D.两点之间线段最短
相关试题

