【题目】如图,在Rt△ABC中,∠ABC=90°,BD⊥AC于点D ,点E为线段BC的中点,AD=2,tan A=2.
(1)求AB的长;
(2)求DE的长.
参考答案:
【答案】
(1)解:∵BD⊥AC,且tan A=2.
∴ ![]() ,
,
∵AD=2,
∴BD=4,
∴AB= ![]()
(2)解:在Rt△ABC中,
∵∠ABC=90°,且tan A=2.
∴ ![]() ,
,
∵AB= ![]() ,
,
∴BC= ![]() ,
,
∵BD⊥AC,且E点为线段BC的中点,
∴DE= ![]() BC=
BC= ![]()
【解析】利用∠ABD的正切值求出BD的长,再利用勾股定理列式进行计算即可求出AB;根据直角三角形斜边上的中线等于斜边的一半可得DE=CE,再根据等边对等角的性质可得∠EDC=∠C,再根据同角的余角相等求出∠C=∠ABD,然后根据锐角的正弦等于对边比斜边列式进行计算即可得解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为6的正方形ABCD中,对角线AC、BD交于点O,E是BC的中点,DE交AC于点F,则OF的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E、F、G、H分别是四边形ABCD的边AB、BC、CD、DA的中点.
(1)如果图中线段都可画成有向线段,那么在这些有向线段所表示的向量中,与向量
 相等的向量是 ;
相等的向量是 ;(2)设
 =
= ,
, =
= ,
, =
= .试用向量
.试用向量 ,
, 或
或 表示下列向量:
表示下列向量: = ;
= ; = .
= .(3)求作:

 .(请在原图上作图,不要求写作法,但要写出结论)
.(请在原图上作图,不要求写作法,但要写出结论)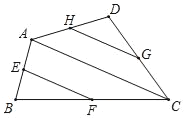
-
科目: 来源: 题型:
查看答案和解析>>【题目】某边防局接到情报,近海处有一可疑船只
 正向公海方向行驶,边防局迅速派出快艇
正向公海方向行驶,边防局迅速派出快艇 追赶(如图1).图2中
追赶(如图1).图2中 、
、 分别表示两船相对于海岸的距离
分别表示两船相对于海岸的距离 (海里)与追赶时间
(海里)与追赶时间 (分)之间的关系.
(分)之间的关系.(1)求
 、
、 的函数解析式;
的函数解析式;(2)当
 逃到离海岸12海里的公海时,
逃到离海岸12海里的公海时, 将无法对其进行检查.照此速度,
将无法对其进行检查.照此速度, 能否在
能否在 逃入公海前将其拦截?若能,请求出此时
逃入公海前将其拦截?若能,请求出此时 离海岸的距离;若不能,请说明理由.
离海岸的距离;若不能,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】化简并求值
(1)5x2y+[7xy﹣2(3xy﹣2x2y)﹣xy],其中x=﹣1,y=﹣

(2)已知a2﹣a﹣2=0,求a2﹣2(a2﹣a+3)﹣
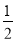 (a2﹣a﹣4)的值.
(a2﹣a﹣4)的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直角梯形
 ,
, ,
, ,过点
,过点 作
作 ,垂足为点
,垂足为点 ,
, ,
, ,点
,点 是
是 边上的一动点,过
边上的一动点,过 作线段
作线段 的垂直平分线,交
的垂直平分线,交 于点
于点 ,并交射线
,并交射线 于点
于点 .
.(1)如图1,当点
 与点
与点 重合时,求
重合时,求 的长;
的长;(2)设
 ,
, ,求
,求 与
与 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;(3)如图2,联结
 ,当
,当 是等腰三角形时,求
是等腰三角形时,求 的长.
的长.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,EF 过平行四边形 ABCD 对角线的交点 O,交 AD 于 E,交 BC 于 F,若平行四边形 ABCD 的周长为32,OE=2,则四边形 ABFE 的周长为__________.

相关试题

