【题目】在Rt△ABC中,∠ACB=90°,AC=15,AB=25,点D为斜边AB上动点.

(1)如图1,当CD⊥AB时,求CD的长度;
(2)如图2,当AD=AC时,过点D作DE⊥AB交BC于点E,求CE的长度;
(3)如图3,在点D的运动过程中,连接CD,当△ACD为等腰三角形时,直接写出AD的长度.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)当△ACD为等腰三角形时,AD的长度为:15或18或
;(3)当△ACD为等腰三角形时,AD的长度为:15或18或![]() .
.
【解析】
(1)由勾股定理求出BC的长度,再由面积法求出CD的长度即可;
(2)连接AE,可证明△ACE≌△ADE,得到CE=DE,设CE=DE=x,则BE=![]() ,由BD=10,则利用勾股定理,求出x,即可得到CE的长度;
,由BD=10,则利用勾股定理,求出x,即可得到CE的长度;
(3)当△ACD为等腰三角形时,可分为三种情况进行①AD=AC;②AC=CD;③AD=CD;对三种情况进行计算,即可得到AD的长度.
解:(1)如图,
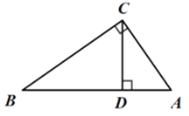
在Rt△ABC中,∠ACB=90°,AC=15,AB=25,
∴BC=![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得:![]() ;
;
(2)如图,连接AE,
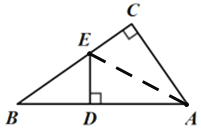
∵DE⊥AB,
∴∠ADE=∠C=90°,
在Rt△ADE和Rt△ACE中,
![]() ,
,
∴Rt△ADE≌Rt△ACE,
∴DE=CE;
设DE=CE=x,则BE=![]() ,又BD=
,又BD=![]()
在Rt△BDE中,由勾股定理,得
![]() ,
,
解得:![]() ,
,
∴![]() ;
;
(3)在Rt△ABC中,有AB=25,AC=15,BC=20,点C到AB的距离为12;
当△ACD为等腰三角形时,可分为三种情况:
①当AD=AC时,AD=15;
②当AC=CD时,如图,作CE⊥AB于点E,则![]() ,
,
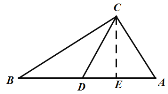
∵CE=12,由勾股定理,得
![]() ,
,
∴![]() ;
;
③当AD=CD时,如图,

在Rt△ABC中,∠ACB=90°,
当点D是AB中点时,有AD=BD=CD,
∴![]() ;
;
综合上述,当△ACD为等腰三角形时,AD的长度为:15或18或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为1的正方形ABCD的对角线AC,BD相交于点O,直角∠MPN的顶点P与点O重合,直角边PM,PN分别与OA,OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是_____.
(1)EF=
 OE;(2)S四边形OEBF:S正方形ABCD=1:4;(3)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=
OE;(2)S四边形OEBF:S正方形ABCD=1:4;(3)在旋转过程中,当△BEF与△COF的面积之和最大时,AE= ;(4)OGBD=AE2+CF2.
;(4)OGBD=AE2+CF2.
-
科目: 来源: 题型:
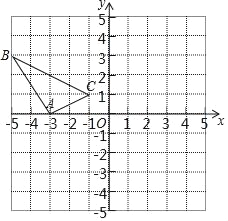
查看答案和解析>>【题目】在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系△ABC是格点三角形(顶点在网格线的交点上)
(1)先作△ABC关于原点O成中心对称的△A1B1C1,再把△A1B1C1向上平移4个单位长度得到△A2B2C2;
(2)△A2B2C2与△ABC是否关于某点成中心对称?若是,直接写出对称中心的坐标;若不是,请说明理由.
-
科目: 来源: 题型:
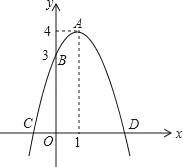
查看答案和解析>>【题目】如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C、D两点.点P是x轴上的一个动点.
(1)求此抛物线的解析式;
(2)当PA+PB的值最小时,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一次数学活动课上,张明用17个边长为1的小正方形搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要 个小立方体,王亮所搭几何体的表面积为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,并且AD是⊙O的直径,C是
 的中点,AB和DC的延长线交于⊙O外一点E.
的中点,AB和DC的延长线交于⊙O外一点E.求证:(1)∠EBC=∠D;
(2)BC=EC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在Rt△ABC中,∠ACB=90°,动点M从点A出发沿A-C-B向点B匀速运动,动点N从点B出发沿B-C-A向点A运动.设MC的长为y1(cm),NC的长为y2(cm),点M的运动时间为x(s);y1、y2与x的函数图像如图2所示.

(1)线段AC= cm,点M运动 s后点N开始运动;
(2)求点P的坐标,并写出它的实际意义;
(3)当∠CMN=45°时,求x的值.
相关试题

