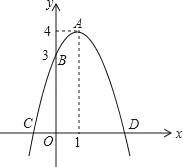
【题目】如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C、D两点.点P是x轴上的一个动点.
(1)求此抛物线的解析式;
(2)当PA+PB的值最小时,求点P的坐标.
参考答案:
【答案】(1) y=-x2+2x+3.(2)( ![]() ,0)
,0)
【解析】试题分析:
(1)由题意可设抛物线解析式为“顶点式”,再代入点B的坐标可求得解析式;
(2)由题意作出点B关于![]() 轴的对称轴点E,连接AE交
轴的对称轴点E,连接AE交![]() 轴于点P,P为所求的点,由A、E的坐标可求得直线AE的解析式,再由AE的解析式就可求得点P的坐标.
轴于点P,P为所求的点,由A、E的坐标可求得直线AE的解析式,再由AE的解析式就可求得点P的坐标.
试题解析:
(1)∵抛物线的顶点A的坐标为(1,4),
∴设抛物线的表达式为y=a(x-1)2+4.
∵抛物线过点B(0,3),
∴3=a(0-1)2+4.
解得a=-1.
∴二次函数的表达式为y=-(x-1)2+4,即y=-x2+2x+3.
(2)作点B关于x轴的对称点E(0,-3),
连接AE交x轴于点P,点P即为所求点.
设AE所在直线的表达式为y=kx+b,
分别代入A,E坐标,得![]() ,解得
,解得![]() ,
,
∴y=7x-3.
当y=0时,x=![]() .
.
∴点P的坐标为(![]() ,0).
,0).
-
科目: 来源: 题型:
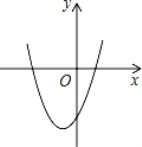
查看答案和解析>>【题目】在平面直角坐标系中,二次函数y=x2+2x﹣3的图象如图所示,点A(x1,y1),B(x2,y2)是该二次函数图象上的两点,其中﹣3≤x1<x2≤0,则下列结论正确的是( )
A. y1<y2B.y1>y2C.y的最小值是﹣3 D.y的最小值是﹣4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,2×2网格(每个小正方形的边长为1)中有A,B,C,D,E,F,G,H,O九个格点.抛物线l的解析式为y=(-1)nx2+bx+c(n为整数).

(1)n为奇数,且l经过点H(0,1)和C(2,1),求b,c的值,并直接写出哪个格点是该抛物线上的顶点;
(2)n为偶数,且l经过点A(1, 0)和B(2,0),通过计算说明点F(0,2)和H(0,1)是否在抛物线上;
(3)若l经过这九个格点中的三个,直接写出满足这样条件的抛物线条数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c与x轴交于点A(1,0),B(3,0),且过点C(0,-3).
(1)求抛物线的解析式和顶点坐标;
(2)请你写出一种平移的方法,使平移后抛物线的顶点落在直线y=-x上,并写出平移后抛物线的解析式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是用火柴棍摆成边长分别是1、2、3根火柴棍时的正方形,当边长为n根火柴棍时,若摆出的正方形所用的火柴棍的根数为S,则S= (用含n的代数式表示,n为正整数).

-
科目: 来源: 题型:
查看答案和解析>>【题目】在学习“二元一次方程组的解”时,数学张老师设计了一个数学活动,有A、B两组卡片,每组各三张,A组卡片上分别写有0,1,2;B组卡片上分别写有-3,-1,1。每张卡片除正面写有不同数字外,其余均相同。甲从A组随机抽取一张记为x,乙从B组随机抽取一张记为y。
(1)若甲抽出的数字是2,乙抽出的数字是-1,它们恰好是方程ax-y=5的解,求a的值;
(2)求甲、乙随机抽取一次的数恰好是方程ax-y=3的解得概率(请用树状图或列表法求解
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组数中:①-22与(-2)2; ②(-3)2与-33; ③-(-32)与-32 ;④02019与02018;⑤(-1)2019与-(-1)2.其中结果相等的数据共有( )
A.1对B.2对C.3对D.4对
相关试题

