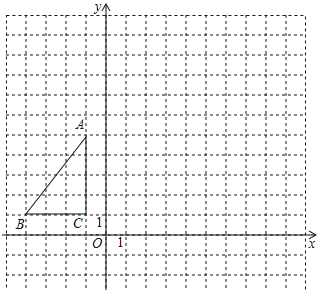
【题目】已知:如图,在8×12的矩形网格中,每个小正方形的边长都为1,四边形ABCD的顶点都在格点上.
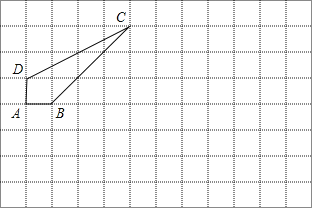
(1)以B为坐标原点,AB所在直线为x轴,建立直角坐标系;
(2)写出四边形各顶点的坐标;
(3)计算四边形的面积;
(4)画出将四边形向右平移5个单位,向下平移2个单位得到的图形.
参考答案:
【答案】(1)见解析;(2)A(﹣1,0),B(0,0),C(3,3),D(﹣1,1);(3)![]() ;(4)见解析
;(4)见解析
【解析】
试题分析:(1)以B为坐标原点建立坐标系即可;
(2)根据平面直角坐标系写出四边形各顶点的坐标即可;
(3)把四边形分成一个三角形和一个梯形,然后再计算两个图形的面积和即可;
(4)首先确定A、B、C、D四个顶点平移后的位置,再连接即可.
解:(1)如图所示:
(2)A(﹣1,0),B(0,0),C(3,3),D(﹣1,1);
(3)四边形ABCD的面积:![]() ×(1+2)×1+
×(1+2)×1+![]() ×2×2=
×2×2=![]() ;
;
(4)如图所示.
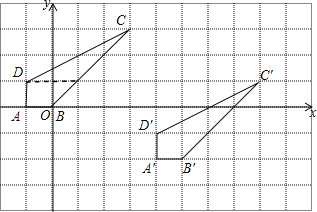
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列几何体中,正视图、左视图、俯视图完全相同的是( )
A.圆柱
B.圆锥
C.棱锥
D.球 -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=- 2x2 - 4x - 5经过平移后得到抛物线y=- 2x2,平移方法是( )
A. 向左平移1个单位,再向下平移3个单位
B. 向左平移1个单位,再向上平移3个单位
C. 向右平移1个单位,再向下平移3个单位
D. 向右平移1个单位,再向上平移3个单位
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,E、F分别是BC、AC的中点,延长BA到点D,使2AD=AB.连接DE,DF.
(1)求证:AF与DE互相平分;
(2)若BC=4,求DF的长.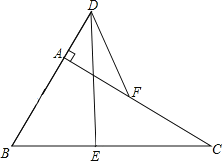
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
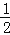 x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).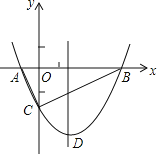
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当△ACM周长最小时,求点M的坐标及△ACM的最小周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,设图中每个小正方形的边长为1,
(1)请画出△ABC关于y轴对称图形△A’B’C’,其中ABC的对称点分别为A’B’C’)
(2)直接写出A’B’C’的坐标:A’B’C’
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC在平面直角坐标系内,顶点的坐标分别为A(﹣1,5),B(﹣4,1),C(﹣1,1)将△ABC绕点A逆时针旋转90°,得到△AB′C′,点B,C的对应点分别为点B′,C′,
(1)画出△AB′C′;
(2)写出点B′,C′的坐标;
(3)求出在△ABC旋转的过程中,点C经过的路径长.
相关试题

