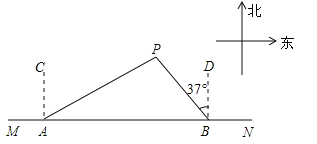
【题目】如图,船A、B在东西方向的海岸线MN上,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东60°方向上,在船B的北偏西37°方向上,AP=30海里.
(1)尺规作图:过点P作AB所在直线的垂线,垂足为E(要求:保留作图痕迹,不写作法);
(2)求船P到海岸线MN的距离(即PE的长);
(3)若船A、船B分别以20海里/时、15海里/时的速度同时出发,匀速直线前往救援,试通过计算判断哪艘船先到达船P处.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
参考答案:
【答案】(1)作图见试题解析;(2)15海里;(3)B船先到达.
【解析】
试题分析:(1)利用直角三角板中90°的直角直接过点P作AB所在直线的垂线即可;
(2)解Rt△APE求出PE即可;
(3)在Rt△BPF中,求出BP,分别计算出两艘船需要的时间,即可作出判断.
试题解析:(1)如图所示:
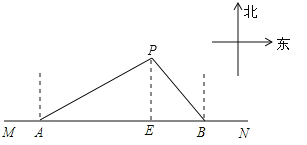
(2)由题意得,∠PAE=30°,AP=30海里,在Rt△APE中,PE=APsin∠PAE=APsin30°=15海里;
(3)在Rt△PBE中,PE=15海里,∠PBE=53°,则BP=![]() 海里,A船需要的时间为:
海里,A船需要的时间为:![]() =1.5小时,B船需要的时间为:
=1.5小时,B船需要的时间为:![]() =1.25小时,∵1.5>1.25,∴B船先到达.
=1.25小时,∵1.5>1.25,∴B船先到达.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,对角线AC,BD相交于点O,且AC⊥BD,点E,F,G,H分别是AB,BC,CD,DA的中点,依次连接各边中点得到四边形EFGH,求证:四边形EFGH是矩形.

-
科目: 来源: 题型:
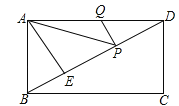
查看答案和解析>>【题目】如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P、Q分别在BD,AD上,则AP+PQ的最小值为( )
A.
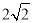 B.
B.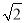 C.
C. D.
D.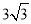
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个工程队参与某小区7200平方米(外墙保温)工程招标,比较这两个工程队的标书发现:乙队每天完成的工程量是甲队的1.5倍,这样乙队单独干比甲队单独干能提前15天完成任务,求甲队在投标书上注明的每天完成的工程量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组,并把解集在数轴上表示出来
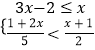 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校体育组对本校九年级全体同学体育测试情况进行调查,他们随机抽查了部分同学体育测试成绩(由高到低分为A、B、C、D四个等级),根据调查的数据绘制成如图的条形统计图和扇形统计图. 请根据以下不完整的统计图提供的信息,解答下列问题:
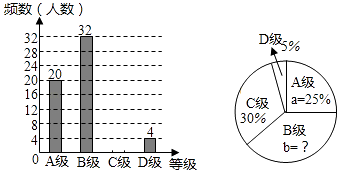
(1)该体育组共抽查了多少名同学的体育测试成绩,扇形统计图中B级所占的百分比b是多少;
(2)补全条形统计图;
(3)若该校九年级共有940名同学,请估计该校九年级同学体育测试达标(测试成绩C级以上,含C级)共多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,DE是△ABC的中位线,延长DE到F,使EF=DE,连接BF

(1)求证:BF=DC;
(2)求证:四边形ABFD是平行四边形.
相关试题

