搜索
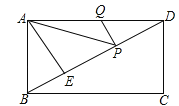
【题目】如图，在矩形ABCD中，AD=6，AE⊥BD，垂足为E，ED=3BE，点P、Q分别在BD，AD上，则AP+PQ的最小值为（ ）
A．
B．
C．
D．
参考答案：
【答案】D．
【解析】
试题分析：
设BE=x，则DE=3x，∵四边形ABCD为矩形，且AE⊥BD，∴△ABE∽△DAE，∴
=BEDE，即
，∴AE=
x，在Rt△ADE中，由勾股定理可得
，即
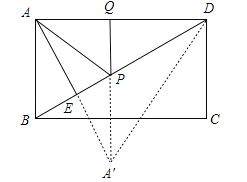
，解得x=，∴AE=3，DE=
，如图，设A点关于BD的对称点为A′，连接A′D，PA′，则A′A=2AE=6=AD，AD=A′D=6，∴△AA′D是等边三角形，∵PA=PA′，∴当A′、P、Q三点在一条线上时，A′P+PQ最小，又垂线段最短可知当PQ⊥AD时，A′P+PQ最小，∴AP+PQ=A′P+PQ=A′Q=DE=，故选D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】矩形具有而菱形不具有的性质是 （ ）
A. 对边相等 B. 对角线互相平分 C. 对角线互相垂直 D. 对角线相等
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB=AC，AD是BC边上的高，AM是△ABC外角∠CAE的平分线．
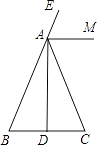
（1）用尺规作图方法，作∠ADC的平分线DN；（保留作图痕迹，不写作法和证明）
（2）设DN与AM交于点F，判断△ADF的形状，并证明你的结论． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中，对角线AC，BD相交于点O，且AC⊥BD，点E，F，G，H分别是AB，BC，CD，DA的中点，依次连接各边中点得到四边形EFGH，求证：四边形EFGH是矩形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两个工程队参与某小区7200平方米（外墙保温）工程招标，比较这两个工程队的标书发现：乙队每天完成的工程量是甲队的1.5倍，这样乙队单独干比甲队单独干能提前15天完成任务，求甲队在投标书上注明的每天完成的工程量．
-
科目： 来源： 题型：
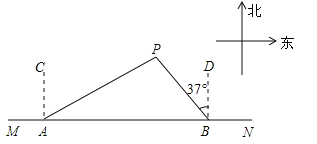
查看答案和解析>>【题目】如图，船A、B在东西方向的海岸线MN上，均收到已触礁搁浅的船P的求救信号，已知船P在船A的北偏东60°方向上，在船B的北偏西37°方向上，AP=30海里．
（1）尺规作图：过点P作AB所在直线的垂线，垂足为E（要求：保留作图痕迹，不写作法）；
（2）求船P到海岸线MN的距离（即PE的长）；
（3）若船A、船B分别以20海里/时、15海里/时的速度同时出发，匀速直线前往救援，试通过计算判断哪艘船先到达船P处．（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）
-
科目： 来源： 题型：
查看答案和解析>>【题目】解不等式组，并把解集在数轴上表示出来
．
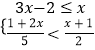相关试题
