【题目】如图在Rt△ABC中,∠C=90°,点D是AC的中点,且∠A+∠CDB=90°,过点A、D作⊙O,使圆心O在AB上,⊙O与AB交于点E.
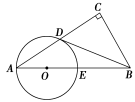
(1)求证:直线BD与⊙O相切;
(2)若AD:AE=4:5,BC=6,求⊙O的直径.
参考答案:
【答案】(1)、证明过程见解析;(2)、5.
【解析】
试题分析:(1)、连接OD,根据△AOD为等腰三角形可得∠A=∠ODA,根据∠A+∠CDB=90°可得∠ODA+∠CDB=90°,从而得出∠BDO=90°;(2)、连接OE,根据直径所对的圆周角为直角得出∠ADE=90°,根据D为中点可得E为AB的中点,根据△ADE和△ACB相似可得AC:AB=4:5,然后求出BC的长度,从而得出直径的长度.
试题解析:(1)、连接OD,在△AOD中,OA=OD, ∴∠A=∠ODA,
又∵∠A+∠CDB=90° ∴∠ODA+∠CDB=90°, ∴∠BDO=180°-90°=90°,即OD⊥BD,
∴BD与⊙O相切.
(2)、连接DE,∵AE是⊙O的直径, ∴∠ADE=90°, ∴DE∥BC.
又∵D是AC的中点,∴AE=BE. ∴△AED∽△ABC.
∴AC∶AB=AD∶AE. ∵AD:AE=4:5 ∴AC∶AB=4∶5,
令AC=4x,AB=5x,则BC=3x. ∵BC=6,∴AB=10,
∴AE=5,∴⊙O的直径为5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组数据:3,5,x,7,9的平均数为6,则x= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:①33°52′+21°54′=;②36°27′×3= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某菜农搭建了一个横截面为抛物线的大棚,尺寸如图:
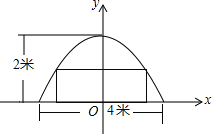
(1)如图建立平面直角坐标系,使抛物线对称轴为y轴,求该抛物线的解析式;
(2)若需要开一个截面为矩形的门(如图所示),已知门的高度为1.60米,那么门的宽度最大是多少米(不考虑材料厚度)?(结果保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于有理数x,我们规定[x]表示不大于x的最大整数,例如[1.2]=1,[3]=3,[﹣2.5]=﹣3.则
①[8.9]=;②[﹣7.9]= . -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是( )
A. 正方形的四条边相等 B. 正方形的四个角相等
C. 平行四边形对角线互相垂直 D. 正方形的对角线相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:2a2﹣8=____________.
相关试题

