【题目】如图,已知一次函数y= ![]() x-3与反比例函数y=
x-3与反比例函数y= ![]() 的图象相交于点A(4,n),与x轴相交于点B.
的图象相交于点A(4,n),与x轴相交于点B.
(1)填空:n的值为 , k的值为;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)观察反比函数y= ![]() 的图象,当y≥-2时,请直接写出自变量x的取值范围.
的图象,当y≥-2时,请直接写出自变量x的取值范围.
参考答案:
【答案】
(1)3,12
(2)解:∵一次函数y= ![]() x-3与x轴相交于点B,
x-3与x轴相交于点B,
∴ ![]() x-3=0,
x-3=0,
解得x=2,
∴点B的坐标为(2,0),
如图,过点A作AE⊥x轴,垂足为E,过点D作DF⊥x轴,垂足为F,
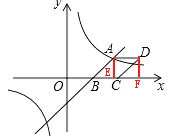
∵A(4,3),B(2,0),
∴OE=4,AE=3,OB=2,
∴BE=OE-OB=4-2=2,
在Rt△ABE中,
AB= ![]() ,
,
∵四边形ABCD是菱形,
∴AB=CD=BC= ![]() ,AB∥CD,
,AB∥CD,
∴∠ABE=∠DCF,
∵AE⊥x轴,DF⊥x轴,
∴∠AEB=∠DFC=90°,
在△ABE与△DCF中,
 ,
,
∴△ABE≌△DCF(ASA),
∴CF=BE=2,DF=AE=3,
∴OF=OB+BC+CF=2+ ![]() +2=4+
+2=4+ ![]() ,
,
∴点D的坐标为(4+ ![]() ,3)
,3)
(3)解:当y=-2时,-2= ![]() ,解得x=-6.
,解得x=-6.
故当y≥-2时,自变量x的取值范围是x≤-6或x>0
【解析】解:(1)把点A(4,n)代入一次函数y= ![]() x-3,可得n=
x-3,可得n= ![]() ×4-3=3;
×4-3=3;
把点A(4,3)代入反比例函数 ![]() ,可得3=
,可得3= ![]() ,
,
解得k=12.
(1)把点A(4,n)代入一次函数,求出n的值,把点A(4,3)代入反比例函数 ,求出k的值;(2)由一次函数与x轴相交于点B,求出点B的坐标,根据已知和勾股定理求出AB的值,由四边形ABCD是菱形,根据菱形的性质,得到△ABE≌△DCF,根据全等三角形的对应边相等,求出DF=AE和OF的值,得到点D的坐标;(3)当y=-2时,求出x的值,得到自变量x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,△ABC为等边三角形,点D,E为直线BC上两动点,且BD=CE.点F,点E关于直线AC成轴对称,连接AE,顺次连接AD,DF,AF.


(1)如图1,若点D、点E在边BC上,试判断∠BAD与∠FDC的大小关系,并说明理由;
(2)若点D、点E在边BC所在的直线上如图(2)所示的位置,(1)中的结论是否还成立,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了培养学生的阅读习惯,某校开展了“读好书,助成长”系列活动,并准备购置一批图书,购书前 ,对学生喜欢阅读的图书类型进行了抽样调查,并将调查数据绘制成两幅不完整的统计图,如图所示,根据统计图所提供的信息,回答下列问题:
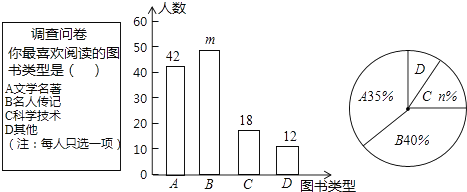
(1)本次调查共抽查了名学生,两幅统计图中的m= , n=.
(2)已知该校共有960名学生,请估计该校喜欢阅读“A”类图书的学生约有多少人?
(3)学校要举办读书知识竞赛,七年(1)班要在班级优胜者2男1女中随机选送2人参赛,求选送的两名参赛学生为1男1女的概率是多少? -
科目: 来源: 题型:
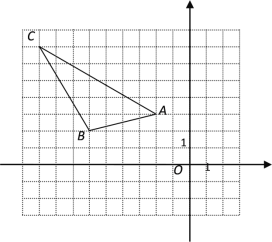
查看答案和解析>>【题目】已知,△ABC在平面直角坐标系中的位置如图所示
(1)、写出A、B、C三点的坐标
(2)、求△ABC的面积
(3)、△ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+4,y0-3),将△ABC作同样的平移得到△A1B1C1,写出A1 、B1、C1的坐标
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三沙市一艘海监船某天在黄岩鸟P附近海域由南向北巡航,某一时刻航行到A处,测得该岛在北偏东30°方向,海监船以20海里/时的速度继续航行,2小时后到达B处,测得该岛在北偏东75°方向,求此时海监船与黄岩岛P的距离BP的长.(参考数据:
 ≈1.414,结果精确到0.1)
≈1.414,结果精确到0.1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,锐角
 中,
中, ,若想找一点P,使得
,若想找一点P,使得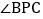 与
与 互补,甲、乙、丙三人作法分别如下:
互补,甲、乙、丙三人作法分别如下:甲:以B为圆心,AB长为半径画弧交AC于P点,则P即为所求;
乙:分别以B,C为圆心,AB,AC长为半径画弧交于P点,则P即为所求;
丙:作BC的垂直平分线和
 的平分线,两线交于P点,则P即为所求.
的平分线,两线交于P点,则P即为所求.对于甲、乙、丙三人的作法,下列叙述正确的是



A. 三人皆正确B. 甲、丙正确,乙错误
C. 甲正确,乙、丙错误D. 甲错误,乙、丙正确
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,以边AB为直径作⊙O,交BC于点D,过D作DE⊥AC于点E.
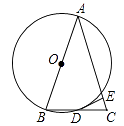
(1)求证:DE为⊙O的切线;
(2)若AB=13,sinB= ,求DE的长.
,求DE的长.
相关试题

