搜索
【题目】已知，△ABC为等边三角形，点D，E为直线BC上两动点，且BD=CE．点F，点E关于直线AC成轴对称，连接AE，顺次连接AD，DF，AF．
（1）如图1，若点D、点E在边BC上，试判断∠BAD与∠FDC的大小关系，并说明理由；
（2）若点D、点E在边BC所在的直线上如图（2）所示的位置，（1）中的结论是否还成立，说明理由．
参考答案：
【答案】（1）
，理由见解析；（2）成立，
，理由见解析．
【解析】
（1）根据等边三角形的性质与判定和全等三角形的判定和性质解答即可；
（2）根据全等三角形的判定和性质以及等边三角形的判定解答即可．
（1），理由如下：
∵
为等边三角形，
∴
，
∵
，
∴
∴
，
，
∵点
，点
关于直线
成轴对称，
∴
，
，
∴
，
，
∵
，
∴
，，
∴
为等边三角形；
∴
∵
又∵
∴
（2）
∵理由：为等边三角形，
∴，
，
∴
∵
∴
∴
，
，
∵点，点关于直线成轴对称，
∴，，
∴，，
∵
，
∴
，∵，
∴为等边三角形，
∴
，
∵
，
∴．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一个不透明的袋中装有除颜色外都相同的球，其中红球5个，白球7个、黑球12个．
（1）求从袋中摸一个球是白球的概率；
（2）现从袋中取出若干个红球，放入相同数量的黑球，使从袋中摸出一个球是黑球的概率不超过60%，问至多取出多少个红球．
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙二人驾车分别从A，B两地同时出发，相向而行．下图是二人离A地的距离y（千米）与所用时间x（小时）的关系．
（1）请说明交点P所表示的实际意义： ；
（2）试求出A，B两地之间的距离；
（3）甲从A地到达B地所需的时间为多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】某手机经销商计划同时购进一批甲、乙两种型号的手机，若购进2部甲型号手机和1部乙型号手机，共需要资金2800元；若购进3部甲型号手机和2部乙型号手机，共需要资金4600元．
（1）求甲、乙型号手机每部进价为多少元；
（2）该店计划购进甲、乙两种型号的手机销售，预计用不多于1.8万元且不少于1.74万元的资金购进这两部手机共20台；若售出一部甲种型号手机，利润率为40%，乙型号手机的售价为1180元．为了获得最多的利润，应如何进货？
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了培养学生的阅读习惯，某校开展了“读好书，助成长”系列活动，并准备购置一批图书，购书前 ，对学生喜欢阅读的图书类型进行了抽样调查，并将调查数据绘制成两幅不完整的统计图，如图所示，根据统计图所提供的信息，回答下列问题：
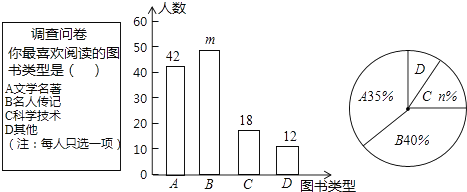
（1）本次调查共抽查了名学生，两幅统计图中的m= ， n=.
（2）已知该校共有960名学生，请估计该校喜欢阅读“A”类图书的学生约有多少人？
（3）学校要举办读书知识竞赛，七年（1）班要在班级优胜者2男1女中随机选送2人参赛，求选送的两名参赛学生为1男1女的概率是多少？ -
科目： 来源： 题型：
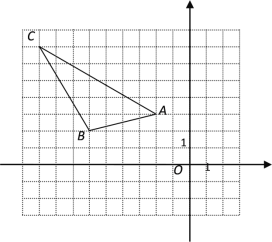
查看答案和解析>>【题目】已知，△ABC在平面直角坐标系中的位置如图所示
(1)、写出A、B、C三点的坐标
(2)、求△ABC的面积
(3)、△ABC中任意一点P（x0，y0）经平移后对应点为P1(x0+4,y0-3),将△ABC作同样的平移得到△A1B1C1，写出A1 、B1、C1的坐标
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知一次函数y=
x-3与反比例函数y= 
的图象相交于点A（4，n），与x轴相交于点B．
（1）填空：n的值为 ， k的值为；
（2）以AB为边作菱形ABCD，使点C在x轴正半轴上，点D在第一象限，求点D的坐标；
（3）观察反比函数y= 的图象，当y≥-2时，请直接写出自变量x的取值范围．
相关试题
