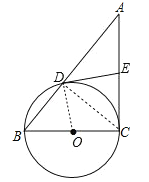
【题目】如图,在Rt△ABC中,∠C=Rt∠,以BC为直径的⊙O交AB于点D,切线DE交AC于点E.
(1)求证:∠A=∠ADE;
(2)若AD=16,DE=10,求BC的长.

参考答案:
【答案】(1)证明见解析;(2)15.
【解析】
试题分析:(1)只要证明∠A+∠B=90°,∠ADE+∠B=90°即可解决问题;
(2)首先证明AC=2DE=20,在Rt△ADC中,DC=![]() =12,设BD=x,在Rt△BDC中,BC2=x2+122,在Rt△ABC中,BC2=(x+16)2﹣202,可得x2+122=(x+16)2﹣202,解方程即可解决问题;
=12,设BD=x,在Rt△BDC中,BC2=x2+122,在Rt△ABC中,BC2=(x+16)2﹣202,可得x2+122=(x+16)2﹣202,解方程即可解决问题;
试题解析:(1)证明:连接OD,∵DE是切线,∴∠ODE=90°,∴∠ADE+∠BDO=90°,∵∠ACB=90°,∴∠A+∠B=90°,∵OD=OB,∴∠B=∠BDO,∴∠ADE=∠A.
(2)连接CD.
∵∠ADE=∠A,∴AE=DE,∵BC是⊙O的直径,∠ACB=90°,∴EC是⊙O的切线,∴ED=EC,∴AE=EC,∵DE=10,∴AC=2DE=20,在Rt△ADC中,DC=![]() =12,设BD=x,在Rt△BDC中,BC2=x2+122,在Rt△ABC中,BC2=(x+16)2﹣202,∴x2+122=(x+16)2﹣202,解得x=9,∴BC=
=12,设BD=x,在Rt△BDC中,BC2=x2+122,在Rt△ABC中,BC2=(x+16)2﹣202,∴x2+122=(x+16)2﹣202,解得x=9,∴BC=![]() =15.
=15.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(x,y)在第一象限内,且x+y=6,点A的坐标为(4,0).设△OPA的面积为S,则下列图象中,能正确反映面积S与x之间的函数关系式的图象是( )
A.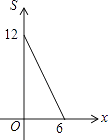
B.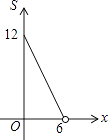
C.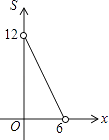
D.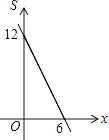
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明用30厘米的铁丝围成一斜边等于13厘米的直角三角形,设该直角三角形一直角边长x厘米,根据题意列方程为
-
科目: 来源: 题型:
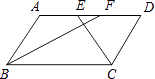
查看答案和解析>>【题目】如图,在ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为( )
A.8
B.10
C.12
D.14 -
科目: 来源: 题型:
查看答案和解析>>【题目】把0.697按四舍五入法精确到0.01的近似值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正数x的平方根是2-m和3m+6,则x的值是__________
-
科目: 来源: 题型:
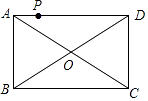
查看答案和解析>>【题目】如图,点P是矩形ABCD的边AD上的一动点,AB=6,BC=8,则点P到矩形的两条对角线AC和BD的距离之和是( )
A.4.8
B.5
C.6
D.7.2
相关试题

