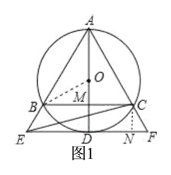
【题目】如图,⊙O是△ABC的外接圆,AD是⊙O的直径,AD与BC相交于点M,且BM=MC,过点D作BC的平行线,分别与AB、AC的延长线相交于点E、F.
(1)求证:EF与⊙O相切;
(2)若BC=2![]() ,MD=
,MD=![]() ,求CE的长.
,求CE的长.

参考答案:
【答案】(1)见解析;(2)![]()
【解析】试题分析:
(1)由AD是⊙O的直径,BM=MC可得AD⊥BC,结合EF∥BC可得AD⊥EF,从而根据“切线的判定定理”可得EF与⊙O相切;
(2)如图1,连接OB,过点C作CN⊥EF于点N.先证△OBM是Rt△,由勾股定理建立方程解此OB的长,因此可得AD的长和AM的长;证△ABC∽△AEF,从而可解得EF的长;在Rt△AMC中,计算出tan∠AMC的值,从而可得∠MAC=30°,由此可得∠NCF=30°,结合CN=MD可在Rt△NCF中解得得NF的长,即可由EN=EF-NF得到EN的长,这样在Rt△ECN中即可由勾股定理解得CE的长了.
试题解析:
(1)∵AD是⊙O的直径,AD与BC相交于点M,且BM=MC,
∴AD⊥BC,
∵EF∥BC,
∴AD⊥EF,
∴EF与⊙O相切;
(2)连接OB,
在△OBM中,BM2+OM2=OB,即(![]() )+(OB﹣
)+(OB﹣![]() )=OB2,OB=2
)=OB2,OB=2![]()
∴OM=MD=![]() ,
,
∵BC∥EF,
∴△ABC∽△AEF
∴![]() ,
,
∴EF=![]() =
=![]() =
=![]() ,
,
∵tan∠CAM=![]() ,
,
∴∠CAM=30°,
作CN⊥EF,
∵AD⊥EF,
∴CN∥AD,
∴∠FCN=∠CAM=30°,
∵BC∥EF,
∴四边形MDNC是矩形,
∴CN=MD=![]() ,
,
∴NF=CNtan30°=![]() ×
×![]() =
=![]() ,
,
∴EN=EF﹣NF=![]() ﹣
﹣![]() =
=![]() ,
,
∴EC=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一元一次方程的根是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.
(1)在方程①3x-1=0;②
 x+1=0;③x-(3x+1)=-5中,不等式组
x+1=0;③x-(3x+1)=-5中,不等式组 关联方程是______(填序号).
关联方程是______(填序号).(2)若不等式组
 的一个关联方程的根是整数,则这个关联方程可以是______(写出一个即可).
的一个关联方程的根是整数,则这个关联方程可以是______(写出一个即可).(3)若方程9-x=2x,3+x=2(x+
 )都是关于x的不等式组
)都是关于x的不等式组 的关联方程,试求出m的取值范围.
的关联方程,试求出m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三角形
 中,
中, ,
, 是
是 上的一点,连接
上的一点,连接 平分
平分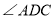 交
交 的外角
的外角 的平分线于
的平分线于 .
.
(1)求证:

(2)若
 ,求
,求 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B(a,b)在第一象限,过B作BA⊥y轴于A,过B作BC⊥x轴于C,且实数a、b满足(a-b-2)2+|2a+b-10|≤0,含45角的Rt△DEF的一条直角边DF与x轴重合,DE⊥x轴于D,点F与坐标原点重合,DE=DF=3.△DEF从某时刻开始沿着坐标轴以1个单位长度每秒的速度匀速运动,运动时间为t秒.
(1)求点B的坐标;
(2)若△DEF沿着y轴负方向运动,连接AE,EG平分∠AEF,EH平分∠AED,当EG∥DF时,求∠HEF的度数;
(3)若△DEF沿着x轴正方向运动,在运动过程中,记△AEF与长方形OABC重叠部分的面积为S,当0<t≤4,S=
 时,请你求出运动时间t.
时,请你求出运动时间t.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了调查学生书写汉字的能力,从八年级800名学生中随机抽选了50名学生参加测试,这50名学生同时听写50个常用汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出不完整的频数分布表和频数分布直方图如图表:
频数分布表
组别
成绩x分
频数(人数)
第1组
25≤x<30
4
第2组
30≤x<35
8
第3组
35≤x<40
16
第4组
40≤x<45
a
第5组
45≤x<50
10
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,请你估计该校八年级汉字书写优秀的人数?
(4)第一组中的A、B、C、D 四名同学为提高汉字书写能力,分成两组,每组两人进行对抗练习,请用列表法或画树状图的方法,求A与B名同学能分在同一组的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A、D、C、F在同一直线上,AB=DE,AD=CF,添加下列条件后,仍不能判断△ABC≌△DEF的是( )

A.
 B.
B. 
C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某飞机模型的机翼形状如图所示,其中AB∥DC,∠BAE=90°,根据图中的数据求CD的长?(精确到1cm)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

相关试题

