【题目】如图,P是线段AB上一点,C、D两点分别从P、B出发以1cm/s、2 cm/s的速度沿直线AB向左运动(C在线段AP上,D在线段BP上)
(1)若C、D运动到任一时刻时,总有PD=2AC,请说明P点在线段AB上的位置: ![]()
(2)在(1)的条件下,Q是直线AB上一点,且AQ-BQ=PQ,求![]() 的值。
的值。
![]()
(3)在(1)的条件下,若C、D运动5秒后,恰好有![]() ,此时C点停止运动,D点继续运动(D点在线段PB上),M、N分别是CD、PD的中点,下列结论:①PM-PN的值不变;②
,此时C点停止运动,D点继续运动(D点在线段PB上),M、N分别是CD、PD的中点,下列结论:①PM-PN的值不变;②![]() 的值不变,可以说明,只有一个结论是正确的,请你找出正确的结论并求值.
的值不变,可以说明,只有一个结论是正确的,请你找出正确的结论并求值.
参考答案:
【答案】(1)点P在线段AB上的![]() 处;(2)
处;(2)![]() ;(3)②
;(3)②![]() 的值不变.
的值不变.
【解析】
(1)根据C、D的运动速度知BD=2PC,再由已知条件PD=2AC求得PB=2AP,所以点P在线段AB上的![]() 处;
处;
(2)由题设画出图示,根据AQ-BQ=PQ求得AQ=PQ+BQ;然后求得AP=BQ,从而求得PQ与AB的关系;
(3)当点C停止运动时,有CD=![]() AB,从而求得CM与AB的数量关系;然后求得以AB表示的PM与PN的值,所以MN=PNPM=
AB,从而求得CM与AB的数量关系;然后求得以AB表示的PM与PN的值,所以MN=PNPM=![]() AB.
AB.
解:(1)由题意:BD=2PC
∵PD=2AC,
∴BD+PD=2(PC+AC),即PB=2AP.
∴点P在线段AB上的![]() 处;
处;
(2)如图:
![]()
∵AQ-BQ=PQ,
∴AQ=PQ+BQ,
∵AQ=AP+PQ,
∴AP=BQ,
∴PQ=![]() AB,
AB,
∴![]()
(3)②![]() 的值不变.
的值不变.
理由:如图,
![]()
当点C停止运动时,有CD=![]() AB,
AB,
∴CM=![]() AB,
AB,
∴PM=CM-CP=![]() AB-5,
AB-5,
∵PD=![]() AB-10,
AB-10,
∴PN=![]() AB-10)=
AB-10)=![]() AB-5,
AB-5,
∴MN=PN-PM=![]() AB,
AB,
当点C停止运动,D点继续运动时,MN的值不变,
所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在平面直角坐标系中,点
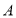 坐标
坐标 ,点
,点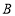 坐标
坐标 ,连接
,连接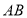 ,
,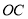 平分
平分 交
交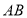 于点
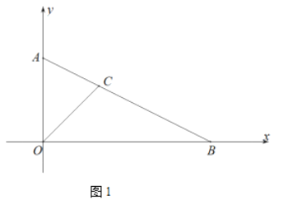
于点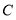 .
.
(1)如图1,求
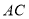 的长;
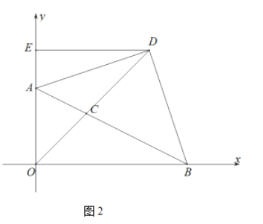
的长;(2)如图2,
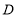 是
是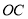 延长线上一点,连接
延长线上一点,连接 ,
,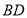 ,且
,且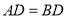 ,过点
,过点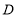 作
作 轴于点
轴于点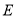 ,若点
,若点 是线段
是线段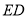 上一点,点
上一点,点 的横坐标为
的横坐标为 ,连接
,连接 ,设
,设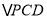 的面积为
的面积为 ,求
,求 与
与 的关系;
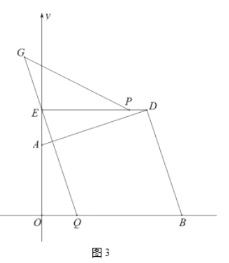
的关系;(3)在(2)的条件下,如图3,线段
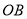 上存在一点
上存在一点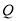 ,使得
,使得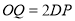 ,点
,点 在
在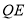 的延长线上,且
的延长线上,且 ,连接
,连接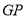 ,若
,若 ,求点
,求点 的坐标及
的坐标及 值?
值? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长分别为1、2、3、5、…的若干正方形按一定的规律拼成不同的长方形,依次记作长方形①、长方形②、长方形③、长方形④,那么按此规律,长方形⑥的周长为_____.
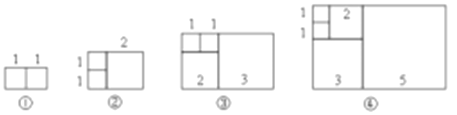
-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车专卖店经销某种型号的汽车.已知该型号汽车的进价为15万元/辆,经销一段时间后发现:当该型号汽车售价定为25万元/辆时,平均每周售出8辆;售价每降低0.5万元,平均每周多售出1辆.
(1)当售价为22万元/辆时,求平均每周的销售利润.
(2)若该店计划平均每周的销售利润是90万元,为了尽快减少库存,求每辆汽车的售价.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有若干个仅颜色不同的红球和黑球,现往一个不透明的袋子里装进4个红球和6个黑球.
(1)若先从袋子里取出m个红球(不放回),再从袋子里随机摸出一个球,将“摸到黑球”记为事件A. 若事件A为必然事件,则m= .
(2)若先从袋子里取出n个黑球,再放入2n个红球,若随机摸出一个球是红球的概率等于2/3,通过计算求n的值.
-
科目: 来源: 题型:
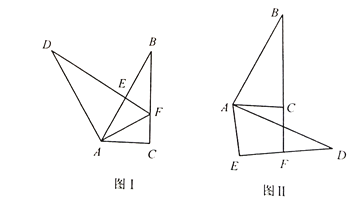
查看答案和解析>>【题目】(1)如图1,在△ABC中,∠ACB=90°,点D在△ABC外,连接AD,作DE⊥AB,交BC于点F,AD=AB,AE=AC,连接AF,则DF,BC,CF间的等量关系是 ;
(2)如图2,AB=AD,AC=AE,∠ACB=∠AED=90°,延长BC交DE于点F,写出DF,BC,CF间的等量关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一元二次方程mx2-2mx+m-2=0.
(1)若方程有两个不等实数根,求m的取值范围;
(2)若方程的两实数根为x1,x2,且|x1-x2|=1,求m的值.
相关试题

