【题目】如图,△ABC各顶点的坐标分别是A(﹣2,﹣4),B(0,﹣4),C(1,﹣1). 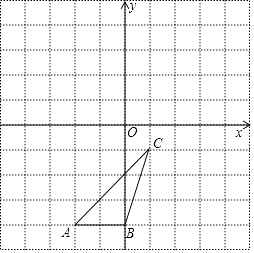
(1)在图中画出△ABC关于原点对称的△AB1C1;
(2)在图中画出△ABC绕原点C逆时针旋转90°后的△A2B2C2;
(3)在(2)的条件下,AC边扫过的面积是 .
参考答案:
【答案】
(1)解:如图,△A1B1C1为所作
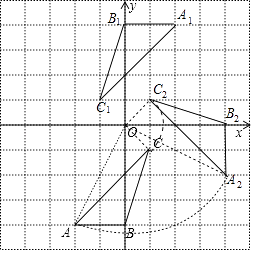
(2)解:如图,△A2B2C2为所作

(3)![]() π
π
【解析】解:(3)OC= ![]() ,OA=
,OA= ![]() =2
=2 ![]() , AC边扫过的面积=S扇形OAA2﹣S扇形OCC2=
, AC边扫过的面积=S扇形OAA2﹣S扇形OCC2= ![]() ﹣
﹣ ![]() =
= ![]() π.
π.
所以答案是 ![]() π.(1)利用关于原点对称的点的坐标特征写出点A1、B1、C1的坐标,然后描点即可得到△A1B1C1;(2)根据网格特点和旋转的性质画出A、B、C对称点A2、B2、C2 , 从而得到△A3B3C3;(3)根据扇形的面积公式,利用AC边扫过的面积=S扇形OAA2﹣S扇形OCC2进行计算即可.
π.(1)利用关于原点对称的点的坐标特征写出点A1、B1、C1的坐标,然后描点即可得到△A1B1C1;(2)根据网格特点和旋转的性质画出A、B、C对称点A2、B2、C2 , 从而得到△A3B3C3;(3)根据扇形的面积公式,利用AC边扫过的面积=S扇形OAA2﹣S扇形OCC2进行计算即可.
【考点精析】解答此题的关键在于理解扇形面积计算公式的相关知识,掌握在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).
-
科目: 来源: 题型:
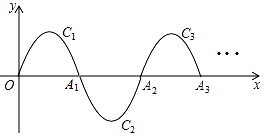
查看答案和解析>>【题目】如图,一条抛物线y=﹣x(x﹣2)(0≤x≤2)的一部分,记为C1 , 它与x轴交于O,A1两点,将C1绕点A1旋转180°得到C2 , 交x轴于点A2 , ;将C2绕点A2旋转180°得到C3 , 交x轴于A3;…如此进行下去,直至得到C6 , 若点P(2017,y)在抛物线Cn上,则y= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程或不等式组
(1)用配方法解方程:x2﹣x=3x+5
(2)解不等式组: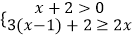 ,并判断﹣1,
,并判断﹣1,  这两个数是否为该不等式组的解.
这两个数是否为该不等式组的解. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=2x2﹣mx﹣m2
(1)求证:对于任意实数m,二次函数y=2x2﹣mx﹣m2的图象与x轴总有公共点;
(2)若这个二次函数图象与x轴有两个公共点A,B,且B点坐标为(1,0),求A点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,O是AB边上的一点,以OA为半径的⊙O与边BC相切于点E.
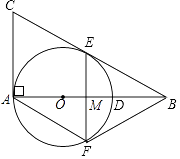
(1)若AC=6,BC=10,求⊙O的半径.
(2)过点E作弦EF⊥AB于M,连接AF,若∠F=2∠B,求证:四边形ACEF是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为6,E,F分别是AB,BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.
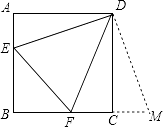
(1)求证:EF=FM.
(2)当AE=2时,求EF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣3,0)两点.

(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;
(3)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若没有,请说明理由.
相关试题

