【题目】如图所示,在直角坐标系中,已知![]() 、
、![]() 、
、![]() 三点,其中
三点,其中![]() 、
、![]() 、
、![]() 满足关系式
满足关系式![]() ,
, ![]() ≤
≤![]() .
.
(1)![]() =_______;
=_______; ![]() =________;
=________; ![]() =_______.
=_______.
(2)如果点![]() 是第二象限内的一个动点,坐标为
是第二象限内的一个动点,坐标为![]() .将四边形
.将四边形![]() 的面积用
的面积用![]() 表示,请你写出
表示,请你写出![]() 关于
关于![]() 的函数表达式,并写出自变量的取值范围.
的函数表达式,并写出自变量的取值范围.
(3)在(2)的条件下,是否存在点![]() ,使得四边形的面积
,使得四边形的面积![]() 与
与![]() 的面积相等?若存在,请求出点
的面积相等?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)2;3;4;(2)S=3-m(m<0);(3)存在,m=-3.
【解析】分析:(1)由非负数的性质求解;(2)由P到线段的OA的距离为![]() ,由三角形面积公式得出结论;(3)据△AOP的面积与△ABC的面积相等可求解.
,由三角形面积公式得出结论;(3)据△AOP的面积与△ABC的面积相等可求解.
本题解析:
(1)a=2,b=3,c=4;
(2)由(1)可知,点 A(0,2),B(3,0),C(3,4) ,
∴OA=2,OB=3,BC=4,
过点P作PE⊥OA ∵P(m, ![]() )在第二象限
)在第二象限
![]() ,
, ![]()
![]()
其中,自变量的取值范围为:m<0
(3)存在; ![]()
根据题意可得, ![]() 则有S=6, ∴3-m=6 则有m=-3
则有S=6, ∴3-m=6 则有m=-3
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于a,b的多项式3(a2-2ab-b2)-(a2+mab+2b2)中不含有ab项,则m=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有下列长度的三条线段,能组成三角形的是( )
A. 2,3,4B. 1,4,2C. 1,2,3D. 6,2,3
-
科目: 来源: 题型:
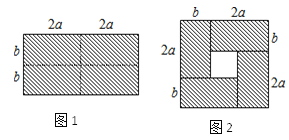
查看答案和解析>>【题目】如图1,将一个长为4a,宽为2b的长方形,沿图中虚线均匀分成4个小长方形,然后按图2形状拼成一个正方形.
(1)图2中的空白部分的边长是多少?(用含a,b的式子表示)
(2)观察图2,请根据图形的面积关系用等式表示出(2a﹣b)2,ab和(2a+b)2之间的数量关系;
(3)若2a+b=7,ab=3,求图2中的空白正方形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校要求八年级同学在课外活动中,必须在五项球类(篮球、足球、排球、羽毛球、乒乓球)活动中任选一项(只能选一项)参加训练,为了了解八年级学生参加球类活动的整体情况,现以八年级2班作为样本,对该班学生参加球类活动的情况进行统计,并绘制了如图所示的不完整统计表和扇形统计图:

根据图中提供的信息,解答下列问题:
(1)a= ,b= ;
(2)该校八年级学生共有600人,则该年级参加足球活动的人数约 人;
(3)该班参加乒乓球活动的5位同学中,有3位男同学(A,B,C)和2位女同学(D,E),现准备从中选取两名同学组成双打组合,用树状图或列表法求恰好选出一男一女组成混合双打组合的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)已知:用2辆A型车和1辆B型车载满货物一次可运货10吨;用1辆A型车和2辆B型车载满货物一次可运货11吨.根据以上信息,解答下列问题:
(1)1辆A型车和1辆车B型车都载满货物一次可分别运货多少吨?
(2)某物流公司现有31吨货物,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满货物.请用含有b的式子表示a,并帮该物流公司设计租车方案;
(3)在(2)的条件下,若A型车每辆需租金100元/次,B型车每辆需租金120元/次.请选出最省钱的租车方案,并求出最少租车费用.
-
科目: 来源: 题型:
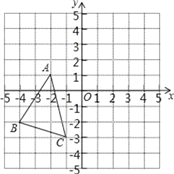
查看答案和解析>>【题目】如图,△ABC中,A(﹣2,1)、B(﹣4,﹣2)、C(﹣1,﹣3),△A′B′C′是△ABC平移之后得到的图象,并且C的对应点C′的坐标为(4,1)
(1)A′、B′两点的坐标分别为A′ 、B′ ;
(2)作出△ABC平移之后的图形△A′B′C′;
(3)求△A′B′C′的面积.
相关试题

