【题目】某校要求八年级同学在课外活动中,必须在五项球类(篮球、足球、排球、羽毛球、乒乓球)活动中任选一项(只能选一项)参加训练,为了了解八年级学生参加球类活动的整体情况,现以八年级2班作为样本,对该班学生参加球类活动的情况进行统计,并绘制了如图所示的不完整统计表和扇形统计图:

根据图中提供的信息,解答下列问题:
(1)a= ,b= ;
(2)该校八年级学生共有600人,则该年级参加足球活动的人数约 人;
(3)该班参加乒乓球活动的5位同学中,有3位男同学(A,B,C)和2位女同学(D,E),现准备从中选取两名同学组成双打组合,用树状图或列表法求恰好选出一男一女组成混合双打组合的概率.

参考答案:
【答案】(1)16,17.5;(2)90;(3)![]() .
.
【解析】
试题分析:(1)首先求得总人数,然后根据百分比的定义求解;
(2)利用总数乘以对应的百分比即可求解;
(3)利用列举法,根据概率公式即可求解.
试题解析:(1)a=5÷12.5%×40%=16,5÷12.5%=7÷b%,∴b=17.5,故答案为:16,17.5;
(2)600×[6÷(5÷12.5%)]=90(人),故答案为:90;
(3)如图,∵共有20种等可能的结果,两名主持人恰为一男一女的有12种情况,∴则P(恰好选到一男一女)=![]() =
=![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】有下列长度的三条线段,能组成三角形的是( )
A. 2,3,4B. 1,4,2C. 1,2,3D. 6,2,3
-
科目: 来源: 题型:
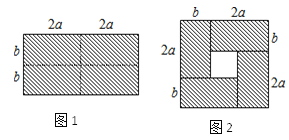
查看答案和解析>>【题目】如图1,将一个长为4a,宽为2b的长方形,沿图中虚线均匀分成4个小长方形,然后按图2形状拼成一个正方形.
(1)图2中的空白部分的边长是多少?(用含a,b的式子表示)
(2)观察图2,请根据图形的面积关系用等式表示出(2a﹣b)2,ab和(2a+b)2之间的数量关系;
(3)若2a+b=7,ab=3,求图2中的空白正方形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在直角坐标系中,已知
 、
、 、
、 三点,其中
三点,其中 、
、 、
、 满足关系式
满足关系式 ,
,  ≤
≤ .
.(1)
 =_______;
=_______;  =________;
=________;  =_______.
=_______.(2)如果点
 是第二象限内的一个动点,坐标为
是第二象限内的一个动点,坐标为 .将四边形
.将四边形 的面积用
的面积用 表示,请你写出
表示,请你写出 关于
关于 的函数表达式,并写出自变量的取值范围.
的函数表达式,并写出自变量的取值范围.(3)在(2)的条件下,是否存在点
 ,使得四边形的面积
,使得四边形的面积 与
与 的面积相等?若存在,请求出点
的面积相等?若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)已知:用2辆A型车和1辆B型车载满货物一次可运货10吨;用1辆A型车和2辆B型车载满货物一次可运货11吨.根据以上信息,解答下列问题:
(1)1辆A型车和1辆车B型车都载满货物一次可分别运货多少吨?
(2)某物流公司现有31吨货物,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满货物.请用含有b的式子表示a,并帮该物流公司设计租车方案;
(3)在(2)的条件下,若A型车每辆需租金100元/次,B型车每辆需租金120元/次.请选出最省钱的租车方案,并求出最少租车费用.
-
科目: 来源: 题型:
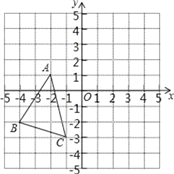
查看答案和解析>>【题目】如图,△ABC中,A(﹣2,1)、B(﹣4,﹣2)、C(﹣1,﹣3),△A′B′C′是△ABC平移之后得到的图象,并且C的对应点C′的坐标为(4,1)
(1)A′、B′两点的坐标分别为A′ 、B′ ;
(2)作出△ABC平移之后的图形△A′B′C′;
(3)求△A′B′C′的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(14分)小明到某服装商场进行社会调查,了解到该商场为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法,并获得如下信息:
营业员A:月销售件数200件,月总收入2400元;
营业员B:月销售件数300件,月总收入2700元;
假设营业员的月基本工资为
 元,销售每件服装奖励
元,销售每件服装奖励 元.
元.(1)求
 、
、 的值;
的值;(2)若某营业员的月总收入不低于3100元,那么他当月至少要卖服装多少件?
(3)商场为了多销售服装,对顾客推荐一种购买方式:如果购买甲3件,乙2件,丙1件共需350元;如果购买甲1件,乙2件,丙3件共需370元.某顾客想购买甲、乙、丙各一件共需多少元?
相关试题

