【题目】如图,AB是⊙O直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,切线GD与AB延长线交于点E.
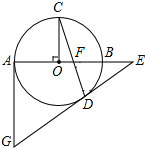
(1)求证:∠C+∠EDF=90°
(2)已知:AG=6,⊙O的半径为3,求OF的值.
参考答案:
【答案】(1)见解析;(2)1
【解析】
试题分析:(1)连接OD,根据切线的性质得OD⊥DE,则∠EDF+∠ODC=90°,而∠C=∠ODC,则∠EDF+∠C=90°.
(2)先求得EF=ED,设DE=x,则EF=x,根据切线的性质由AG为⊙O的切线得∠ODE=90°,再证明Rt△EOD∽Rt△EGA,利用相似比求得AE=2x,OE=3+![]() x,然后根据AE﹣OE=OA=3,求得x的值,进而求得OF=1.
x,然后根据AE﹣OE=OA=3,求得x的值,进而求得OF=1.
(1)证明:连接OD,
∵DE为⊙O的切线,
∴OD⊥DE,
∴∠ODE=90°,即∠EDF+∠ODC=90°,
∵OC=OD,
∴∠C=∠ODC,
∴∠C+∠EDF=90°.
(2)解:∵∠C+∠EDF=90°,∠C+∠CFO=90°,∠CFO=∠EFD,
∴∠EFD=∠EDF,
∴EF=ED,
设DE=x,则EF=x,
∵∠ODE=∠GAE,∠OED=∠GEA,
∴Rt△EOD∽Rt△EGA,
∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,
,
∴AE=2x,OE=3+![]() x,
x,
∵AE﹣OE=OA=3,
∴2x﹣(3+![]() x)=3,解得x=4,
x)=3,解得x=4,
∴AE=2x=8,
∴OF=AE﹣EF﹣OA=8﹣3﹣4=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】写出一个解为x=2的一元一次方程 .
-
科目: 来源: 题型:
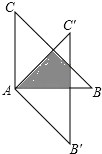
查看答案和解析>>【题目】如图,△ABC绕点A顺时针旋转45°得到△A′B′C′,若∠BAC=90°,AB=AC=2,则图中阴影部分的面积等于 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(3,1)关于x轴的对称点P′的坐标是_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程(2m﹣6)x|m﹣2|﹣2=0是一元一次方程,则m= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A、B均在函数y=
 (k>0,x>0)的图象上,⊙A与x轴相切,⊙B与y轴相切.若点B的坐标为(1,6),⊙A的半径是⊙B的半径的2倍,则点A的坐标为( )
(k>0,x>0)的图象上,⊙A与x轴相切,⊙B与y轴相切.若点B的坐标为(1,6),⊙A的半径是⊙B的半径的2倍,则点A的坐标为( )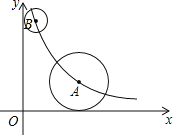
A.(2,2) B.(2,3) C.(3,2) D.(4,
 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如果∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式子中:①90°﹣∠β;②∠α﹣90°;③
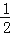 (∠α+∠β);④
(∠α+∠β);④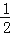 (∠α﹣∠β).正确的有( )
(∠α﹣∠β).正确的有( )A.4个 B.3个 C.2个 D.1个
相关试题

