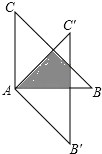
【题目】如图,△ABC绕点A顺时针旋转45°得到△A′B′C′,若∠BAC=90°,AB=AC=2,则图中阴影部分的面积等于 .
参考答案:
【答案】2![]() ﹣2.
﹣2.
【解析】
试题分析:AC′与BC交于点D,B′C′与BC交于点E,与AB交于点F,如图,由∠BAC=90°,AB=AC=2可判断△ABC为等腰直角三角形,则∠B=∠C=45°,BC=![]() AB=2
AB=2![]() ,再根据旋转的性质得∠CAC′=45°,AC′=AC=2,∠C=∠C′=45°,则∠ADC=90°,所以AD=
,再根据旋转的性质得∠CAC′=45°,AC′=AC=2,∠C=∠C′=45°,则∠ADC=90°,所以AD=![]() BC=
BC=![]() ,可计算出C′D=AC′﹣AD=2﹣
,可计算出C′D=AC′﹣AD=2﹣![]() ,接着证明△C′DE为等腰直角三角形得到C′D=DE=2﹣
,接着证明△C′DE为等腰直角三角形得到C′D=DE=2﹣![]() ,证明△AC′F为等腰直角三角形得到C′F=AF=
,证明△AC′F为等腰直角三角形得到C′F=AF=![]() AC′=
AC′=![]() ,然后利用图中阴影部分的面积=S△AC′F﹣S△DC′E进行计算即可.
,然后利用图中阴影部分的面积=S△AC′F﹣S△DC′E进行计算即可.
解:AC′与BC交于点D,B′C′与BC交于点E,与AB交于点F,如图,
∵∠BAC=90°,AB=AC=2,
∴△ABC为等腰直角三角形,
∴∠B=∠C=45°,BC=![]() AB=2
AB=2![]() ,
,
∵△ABC绕点A顺时针旋转45°得到△A′B′C′,
∴∠CAC′=45°,AC′=AC=2,∠C=∠C′=45°,
∴∠ADC=90°,即AD⊥BC,
∴AD=![]() BC=
BC=![]() ,
,
∴C′D=AC′﹣AD=2﹣![]() ,
,
∵△C′DE为等腰直角三角形,
∴C′D=DE=2﹣![]() ,
,
∵∠BAD=90°﹣∠CAC′=45°,
而∠C′=45°,
∴△AC′F为等腰直角三角形,
∴C′F=AF=![]() AC′=
AC′=![]() ,
,
∴图中阴影部分的面积=S△AC′F﹣S△DC′E
=![]() (
(![]() )2﹣
)2﹣![]() (2﹣
(2﹣![]() )2
)2
=2![]() ﹣2.
﹣2.
故答案为2![]() ﹣2.
﹣2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程或方程组解应用题:
近年来,我国逐步完善养老金保险制度.甲、乙两人计划用相同的年数分别缴纳养老保险金15万元和10万元,甲计划比乙每年多缴纳养老保险金0.2万元.求甲、乙两人计划每年分别缴纳养老保险金多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中:①x+3=5﹣x;②﹣5﹣4=﹣9;③3x2﹣2x=4x;④x=5,是一元一次方程的有 (写出对应的序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】写出一个解为x=2的一元一次方程 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(3,1)关于x轴的对称点P′的坐标是_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,切线GD与AB延长线交于点E.
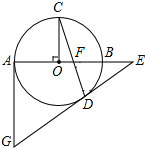
(1)求证:∠C+∠EDF=90°
(2)已知:AG=6,⊙O的半径为3,求OF的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程(2m﹣6)x|m﹣2|﹣2=0是一元一次方程,则m= .
相关试题

