【题目】某校为组织代表队参加市“拜炎帝、诵经典”吟诵大赛,初赛后对选手成绩进行了整理,分成5个小组(x表示成绩,单位:分),A组:75≤x<80;B组:80≤x<85;C组:85≤x<90;D组:90≤x<95;E组:95≤x<100.并绘制出如图两幅不完整的统计图.

请根据图中信息,解答下列问题:
(1)参加初赛的选手共有 名,请补全频数分布直方图;
(2)扇形统计图中,C组对应的圆心角是多少度?E组人数占参赛选手的百分比是多少?
(3)学校准备组成8人的代表队参加市级决赛,E组6名选手直接进入代表队,现要从D组中的两名男生和两名女生中,随机选取两名选手进入代表队,请用列表或画树状图的方法,求恰好选中一名男生和一名女生的概率.
参考答案:
【答案】(1)40;(2)108°,15%;(3)![]() .
.
【解析】试题分析:(1)用A组人数除以A组所占百分比得到参加初赛的选手总人数,用总人数乘以B组所占百分比得到B组人数,从而补全频数分布直方图;
(2)用360度乘以C组所占百分比得到C组对应的圆心角度数,用E组人数除以总人数得到E组人数占参赛选手的百分比;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与恰好抽到一男生和一女生的情况,再利用概率公式即可求得答案.
试题解析:解:(1)参加初赛的选手共有:8÷20%=40(人),B组有:40×25%=10(人).
频数分布直方图补充如下:
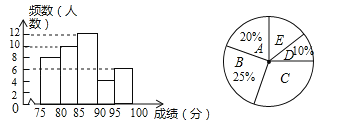
故答案为:40;
(2)C组对应的圆心角度数是:360°×![]() =108°,E组人数占参赛选手的百分比是:
=108°,E组人数占参赛选手的百分比是: ![]() ×100%=15%;
×100%=15%;
(3)画树状图得:
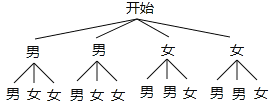
∵共有12种等可能的结果,抽取的两人恰好是一男生和一女生的有8种结果,∴抽取的两人恰好是一男生和一女生的概率为![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E.
(1)求证:AD平分∠BAC;
(2)若CD=1,求图中阴影部分的面积(结果保留π).

-
科目: 来源: 题型:
查看答案和解析>>【题目】为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.
(1)求足球和篮球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和篮球共20个,但要求购买足球和篮球的总费用不超过1550元,学校最多可以购买多少个足球?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,AD、BD、CD分别平分
,AD、BD、CD分别平分 的外角
的外角 ,内角
,内角 ,外角
,外角 ,以下结论:①
,以下结论:① ;②
;② ;③
;③ ;④
;④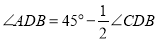 ,其中正确的结论有__.
,其中正确的结论有__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人骑自行车前往A地,他们距A地的路程s(km)与行驶时间t(h)之间的关系如图所示,请根据图象所提供的信息解答下列问题:

(1)甲、乙两人的速度各是多少?
(2)求出甲距
 地的路程
地的路程 与行驶时间
与行驶时间 之间的函数关系式.
之间的函数关系式.(3)在什么时间段内乙比甲离
 地更近?
地更近? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 是等边三角形
是等边三角形 内一点,
内一点, 将
将 绕点
绕点 .按顺时针方向旋转
.按顺时针方向旋转 得
得 , 连接
, 连接 .
.(1)求证:
 是等边三角形;
是等边三角形; (2)当
 时, 试判断
时, 试判断 的形状,并说明理由;
的形状,并说明理由; (3)探究:当
 为多少度时,
为多少度时, 是等腰三角形.
是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】风电已成为我国继煤电、水电之后的第三大电源,风电机组主要由塔杆和叶片组成(如图1),图2是从图1引出的平面图.假设你站在A处测得塔杆顶端C的仰角是55°,沿HA方向水平前进43米到达山底G处,在山顶B处发现正好一叶片到达最高位置,此时测得叶片的顶端D(D、C、H在同一直线上)的仰角是45°.已知叶片的长度为35米(塔杆与叶片连接处的长度忽略不计),山高BG为10米,BG⊥HG,CH⊥AH,求塔杆CH的高.(参考数据:tan55°≈1.4,tan35°≈0.7,sin55°≈0.8,sin35°≈0.6)

相关试题

