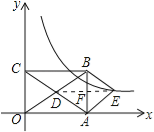
【题目】如图,在平面直角坐标系中,矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB,
(1)求证:四边形AEBD是菱形;
(2)如果OA=3,OC=2,求出经过点E的反比例函数解析式.

参考答案:
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)先证明四边形AEBD是平行四边形,再由矩形的性质得出DA=DB,即可证出四边形AEBD是菱形;
(2)连接DE,交AB于F,由菱形的性质得出AB与DE互相垂直平分,求出EF、AF,得出点E的坐标;设经过点E的反比例函数解析式为:y=![]() ,把点E坐标代入求出k的值即可.
,把点E坐标代入求出k的值即可.
(1)证明:∵BE∥AC,AE∥OB,
∴四边形AEBD是平行四边形,
∵四边形OABC是矩形,
∴DA=![]() AC,DB=
AC,DB=![]() OB,AC=OB,AB=OC=2,
OB,AC=OB,AB=OC=2,
∴DA=DB,
∴四边形AEBD是菱形;
(2)解:连接DE,交AB于F,如图所示:
∵四边形AEBD是菱形,
∴AB与DE互相垂直平分,
∵OA=3,OC=2,
∴EF=DF=![]() OA=
OA=![]() ,AF=
,AF=![]() AB=1,3+
AB=1,3+![]() =
=![]() ,
,
∴点E坐标为:(![]() ,1),
,1),
设经过点E的反比例函数解析式为:y=![]() ,
,
把点E(![]() ,1)代入得:k=
,1)代入得:k=![]() ,
,
∴经过点E的反比例函数解析式为:y=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在函数y=
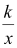 (k>0,x>0)的图象上,点D的坐标为(4,3).
(k>0,x>0)的图象上,点D的坐标为(4,3).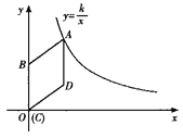
(1)求k的值;
(2)若将菱形ABCD沿x轴正方向平移,当菱形的顶点D落在函数y=
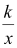 (k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离.
(k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度;已知△ABC.
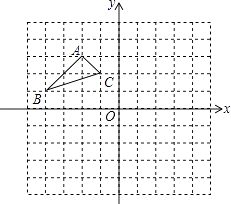
(1)作出△ABC以O为旋转中心,顺时针旋转90°的△A1B1C1 , (只画出图形).
(2)作出△ABC关于原点O成中心对称的△A2B2C2 , (只画出图形),写出B2和C2的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O逆时针方向旋转90°
得到△OA1B1 .
(1)线段A1B1的长是 , ∠AOA1的度数是;
(2)连结AA1 , 求证:四边形OAA1B1是平行四边形;
(3)求四边形OAA1B1的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】在下面给出的数轴中,点 A 表示 1,点 B 表示-2,回答下面的问题:
(1)A、B 之间的距离是 ;
(2)观察数轴,与点 A 的距离为 5 的点表示的数是: ;
(3)若将数轴折叠,使点 A 与-3 表示的点重合,则点 B 与数 表示的点重合;
(4)若数轴上 M、N 两点之间的距离为 2018(M 在 N 的左侧),且 M、N 两点经过(3)中折 叠 后 互 相 重 合 , 则 M 、 N 两 点 表 示 的 数 分 别 是 : M : ;N: .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过反比例函数y=
 (x>0)的图象上一点A作x轴的平行线,交双曲线y=-
(x>0)的图象上一点A作x轴的平行线,交双曲线y=- (x<0)于点B,过B作BC∥OA交双曲线y=-
(x<0)于点B,过B作BC∥OA交双曲线y=- (x<0)于点D,交x轴于点C,连接AD交y轴于点E,若OC=3,求OE的长.
(x<0)于点D,交x轴于点C,连接AD交y轴于点E,若OC=3,求OE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A=3a2b﹣2ab2+abc,小明同学错将“2A﹣B“看成”2A+B“,算得结果为4a2b﹣3ab2+4abc.
(1)计算B的表达式;
(2)求出2A﹣B的结果;
(3)小强同学说(2)中的结果的大小与c的取值无关,对吗?若a=
 ,b=
,b= ,
,求(2)中式子的值.
相关试题

