【题目】如图①,在![]() 中,
中,![]() ,过
,过![]() 上一点
上一点![]() 作
作![]() 交
交![]() 于点
于点![]() ,以
,以![]() 为顶点,
为顶点,![]() 为一边,作
为一边,作![]() ,另一边
,另一边![]() 交
交![]() 于点
于点![]() .
.

(1)求证:四边形![]() 为平行四边形;
为平行四边形;
(2)当点![]() 为
为![]() 中点时,
中点时,![]() 的形状为 ;
的形状为 ;
(3)延长图①中的![]() 到点
到点![]() 使
使![]() 连接
连接![]() 得到图②,若
得到图②,若![]() 判断四边形
判断四边形![]() 的形状,并说明理由.
的形状,并说明理由.

参考答案:
【答案】(1)证明见解析;(2)菱形;(3)四边形![]() 是矩形,理由见解析.
是矩形,理由见解析.
【解析】
(1)根据平行线的性质得到![]() ,根据题意得到
,根据题意得到![]() ,根据平行线的判定定理得到
,根据平行线的判定定理得到![]() ,根据平行四边形的判定定理证明;
,根据平行四边形的判定定理证明;
(2)根据三角形中位线定理得到![]() ,得到
,得到![]() ,根据菱形的判定定理证明;
,根据菱形的判定定理证明;
(3)根据等腰三角形的性质得到![]() ,根据有一个角是直角的平行四边形是矩形证明.
,根据有一个角是直角的平行四边形是矩形证明.
(1)证明:![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,又
,又![]() ,
,
![]() 四边形
四边形![]() 为平行四边形;
为平行四边形;
(2)解:![]() 的形状为菱形,
的形状为菱形,
理由如下:![]() 点
点![]() 为
为![]() 中点,
中点,
![]() ,
,
![]() ,点
,点![]() 为
为![]() 中点,
中点,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 平行四边形
平行四边形![]() 为菱形,
为菱形,
故答案为:菱形;
(3)四边形![]() 是矩形,
是矩形,
理由如下:由(1)得,四边形![]() 为平行四边形,
为平行四边形,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() ,
,![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是矩形.
是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某年级共有300名学生.为了解该年级学生A,B两门课程的学习情况,从中随机抽取60名学生进行测试,获得了他们的成绩(百分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息.
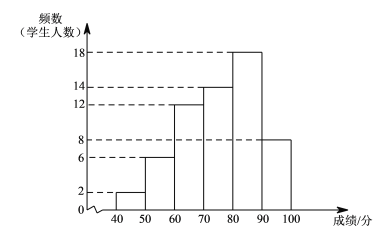
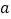 .A课程成绩的频数分布直方图如下(数据分成6组:
.A课程成绩的频数分布直方图如下(数据分成6组: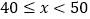 ,
, ,
,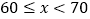 ,
,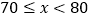 ,
,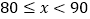 ,
, );
);
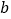 .A课程成绩在
.A课程成绩在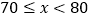 这一组是:
这一组是:70 71 71 71 76 76 77 78
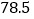
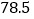 79 79 79
79 79 79 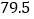
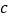 .A,B两门课程成绩的平均数、中位数、众数如下:
.A,B两门课程成绩的平均数、中位数、众数如下:课程
平均数
中位数
众数
A
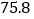
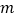
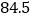
B
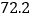
70
83
根据以上信息,回答下列问题:
(1)写出表中
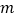 的值;
的值;(2)在此次测试中,某学生的A课程成绩为76分,B课程成绩为71分,这名学生成绩排名更靠前的课程是________(填“A”或“B”),理由是_______;
(3)假设该年级学生都参加此次测试,估计A课程成绩超过
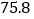 分的人数.
分的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校研究性学习小组在学习二次根式
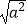 =|a|之后,研究了如下四个问题,其中错误的是( )
=|a|之后,研究了如下四个问题,其中错误的是( )
A.在a>1的条件下化简代数式a+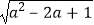 的结果为2a﹣1
的结果为2a﹣1
B.当a+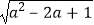 的值恒为定值时,字母a的取值范围是a≤1
的值恒为定值时,字母a的取值范围是a≤1
C.a+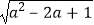 的值随a变化而变化,当a取某个数值时,上述代数式的值可以为
的值随a变化而变化,当a取某个数值时,上述代数式的值可以为 
D.若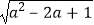 =(
=( 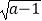 )2 , 则字母a必须满足a≥1
)2 , 则字母a必须满足a≥1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠1=∠2,G为AD的中点,BG的延长线交AC于点E,F为AB上的一点,CF与AD垂直,交AD于点H,则下面判断正确的有( )

①AD是△ABE的角平分线;②BE是△ABD的边AD上的中线;
③CH是△ACD的边AD上的高;④AH是△ACF的角平分线和高
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
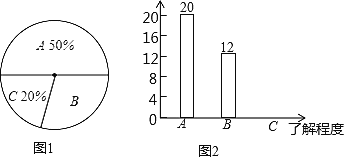
查看答案和解析>>【题目】双峰县教育局要求各学校加强对学生的安全教育,全县各中小学校引起高度重视,小刚就本班同学对安全知识的了解程度进行了一次调查统计.他将统计结果分为三类,A:熟悉;B:了解较多;C:一般了解。图①和图②是他采集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息解答以下问题:
(1)求小刚所在的班级共有多少名学生;
(2)在条形图中,将表示“一般了解”的部分补充完整‘’
(3)在扇形统计图中,计算“了解较多”部分所对应的扇形圆心角的度数;
(4)如果小刚所在年级共1000名同学,请你估算全年级对安全知识“了解较多”的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题:
(1) +|1﹣
+|1﹣  |﹣π0+
|﹣π0+ 
(2)( +
+  )×
)×  ﹣(4
﹣(4  ﹣3
﹣3  )÷2
)÷2  .
. -
科目: 来源: 题型:
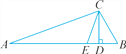
查看答案和解析>>【题目】如图,在△ABC中,CD⊥AB于点D,CE是∠ACB的平分线,∠A=20°,∠B=60°,求∠BCD和∠ECD的度数.
相关试题

