【题目】已知:![]() ,
,![]() 是关于
是关于![]() 的方程
的方程![]() 的两个不相等的实数根,当
的两个不相等的实数根,当![]() 取最小整数时,则
取最小整数时,则![]() 的值为________.
的值为________.
参考答案:
【答案】-2015
【解析】
根据一元二次方程的定义和判别式的意义得到m-1≠0且△=22-4(m-1)(-1)>0,解不等式求出m>0且m≠1,那么m满足条件的最小整数为2,则原方程化为x2+2x-1=0,再根据一元二次方程的解的定义以及根与系数的关系得出a2+2a-1=0,a+b=-2,即a2+2a=1,然后将a3-a2+7b-1998变形为a(a2+2a)-3a2+7b-1998=a-3a2+7b-1998=-3(a2+2a)+7(a+b)-1998,代入计算即可.
根据题意得m1≠0且△=224(m1)(1)>0,
解得m>0且m≠1;
所以m满足条件的最小整数为2,则原方程化为x2+2x1=0,
∵a,b是方程的两个根,
∴a2+2a1=0,a+b=2,
∴a2+2a=1,
a3a2+7b1998
=a(a2+2a)3a2+7b1998
=a3a2+7b1998
=3(a2+2a)+7a+7b1998
=3+7(a+b)1998
=3+7×(2)1998
=2015.
故答案为:2015.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 、
、 两组卡片共
两组卡片共 张,
张, 中三张分别写有数字
中三张分别写有数字 ,
, ,
, ,
, 中两张分别写有
中两张分别写有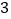 ,
, .它们除了数字外没有任何区别.
.它们除了数字外没有任何区别. 随机地从
随机地从 中抽取一张,求抽到数字为
中抽取一张,求抽到数字为 的概率;
的概率;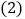 随机地分别从
随机地分别从 、
、 中各抽取一张,请你用画树状图或列表的方法表示所有等可能的结果,现制定这样一个游戏规则:若选出的两数之积为
中各抽取一张,请你用画树状图或列表的方法表示所有等可能的结果,现制定这样一个游戏规则:若选出的两数之积为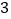 的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?
的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么? 如果不公平请你修改游戏规则使游戏规则对甲乙双方公平.
如果不公平请你修改游戏规则使游戏规则对甲乙双方公平. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场为了吸引顾客,设立了一个可以自由转动的转盘,并规定顾客消费
 元以上,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红、黄或绿色区域,顾客就可以分别获得
元以上,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红、黄或绿色区域,顾客就可以分别获得 元,
元, 元、
元、 元的购物券(转盘被等分成
元的购物券(转盘被等分成 个扇形).
个扇形). 顾客张吉祥消费
顾客张吉祥消费 元,他获得购物券的概率是多少?
元,他获得购物券的概率是多少? 他得到
他得到 元,
元, 元、
元、 元购物券的概率分别是多少?
元购物券的概率分别是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一条长
 米,宽
米,宽 米的矩形草地上修三条小路,小路都等宽,除小路外,草地面积为
米的矩形草地上修三条小路,小路都等宽,除小路外,草地面积为 米2的
米2的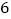 个矩形小块,则小路的宽度应为( )
个矩形小块,则小路的宽度应为( )
A.
 米或
米或 米 B.
米 B.  米 C.
米 C. 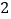 米 D.
米 D.  米
米 -
科目: 来源: 题型:
查看答案和解析>>【题目】某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球多15元,王老师从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球,共花费255元.
(1)该网店甲、乙两种羽毛球每筒的售价各是多少元?
(2)根据消费者需求,该网店决定用不超过8780元购进甲、乙两种羽毛球共200筒,且甲种羽毛球的数量大于乙种羽毛球数量的
 ,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.
,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.①若设购进甲种羽毛球m筒,则该网店有哪几种进货方案?
②若所购进羽毛球均可全部售出,请求出网店所获利润W(元)与甲种羽毛球进货量m(筒)之间的函数关系式,并说明当m为何值时所获利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人共同计算一道整式:(x+a)(2x+b),由于甲抄错了a的符号,得到的结果是2x2-7x+3,乙漏抄了第二个多项式中x的系数,得到的结果是x2+2x-3.
(1)求a,b的值;(2)请计算这道题的正确结果
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形两边长分别是
 和
和 ,第三边的长是一元二次方程
,第三边的长是一元二次方程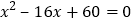 的一个实数根,则此三角形的外接圆半径为________.
的一个实数根,则此三角形的外接圆半径为________.
相关试题

