【题目】三角形两边长分别是![]() 和
和![]() ,第三边的长是一元二次方程
,第三边的长是一元二次方程![]() 的一个实数根,则此三角形的外接圆半径为________.
的一个实数根,则此三角形的外接圆半径为________.
参考答案:
【答案】![]() 或
或![]()
【解析】
先解方程,根据三角形的三边关系可知,方程的两个解都能和已知的两边构建成新的三角形,因此求此三角形的外接圆半径时,有两种情况:第一种情况:三边分别为6、8、10,是直角三角形,所以其斜边就是外接圆的直径,第二种情况:三边分别为6、6、8,等腰三角形,其外接圆的圆心是任意两边垂直平分线的交点,确定其圆心,利用勾股定理列方程可求其半径.
x216x+60=0,
(x10)(x6)=0,
x=10或6,
当第三边为10时,因为![]()
∴此三角形是直角三角形,如图1,
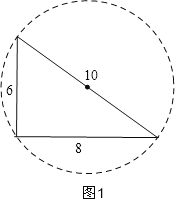
此三角形的外接圆的直径为最大边10,
则此三角形的外接圆半径为5,
当第三边为6时,如图2,
过A作AD⊥BC,垂足为D,作AC的垂直平分线EF,交AC于E,交AD于F,则AF=FC,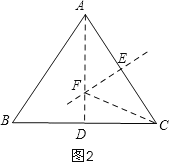
∵AB=AC=6,
∴![]()
∴AD是BC的垂直平分线,
∴F是△ABC外接圆的圆心,FC为外接圆的半径,
由勾股定理得:![]()
设FC=x,则AF=x,![]()
由勾股定理得:![]()
x=![]() ,
,
综上所述,则此三角形的外接圆半径为5或![]() .
.
故答案为:![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
 ,
, 是关于
是关于 的方程
的方程 的两个不相等的实数根,当
的两个不相等的实数根,当 取最小整数时,则
取最小整数时,则 的值为________.
的值为________. -
科目: 来源: 题型:
查看答案和解析>>【题目】某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球多15元,王老师从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球,共花费255元.
(1)该网店甲、乙两种羽毛球每筒的售价各是多少元?
(2)根据消费者需求,该网店决定用不超过8780元购进甲、乙两种羽毛球共200筒,且甲种羽毛球的数量大于乙种羽毛球数量的
 ,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.
,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.①若设购进甲种羽毛球m筒,则该网店有哪几种进货方案?
②若所购进羽毛球均可全部售出,请求出网店所获利润W(元)与甲种羽毛球进货量m(筒)之间的函数关系式,并说明当m为何值时所获利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人共同计算一道整式:(x+a)(2x+b),由于甲抄错了a的符号,得到的结果是2x2-7x+3,乙漏抄了第二个多项式中x的系数,得到的结果是x2+2x-3.
(1)求a,b的值;(2)请计算这道题的正确结果
-
科目: 来源: 题型:
查看答案和解析>>【题目】把一张边长为40 cm的正方形硬纸板,进行适当的裁剪,折成一个长方体盒子(纸板的厚度忽略不计).
(1)如图,若在正方形硬纸板的四角各剪掉一个同样大小的正方形,将剩余部分折成一个无盖的长方体盒子.

①要使折成的长方体盒子的底面积为484 cm2,那么剪掉的正方形的边长为多少?
②折成的长方体盒子的侧面积是否有最大值?如果有,求出这个最大值和此时剪掉的正方形的边长;如果没有,说明理由.
(2)若在正方形硬纸板的四周剪掉一些矩形(即剪掉的矩形至少有一条边在正方形硬纸板的边上),将剩余部分折成一个有盖的长方体盒子.若折成的一个长方体盒子的表面积为550 cm2,求此时长方体盒子的长、宽、高(只需求出符合要求的一种情况).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 是线段
是线段 上的任意一点(端点除外),分别以
上的任意一点(端点除外),分别以 ,
, 为斜边并且在
为斜边并且在 的同一侧作等腰直角
的同一侧作等腰直角 和
和 ,连接
,连接 交
交 于点
于点 ,连接
,连接 交
交 于点
于点 ,给出以下三个结论:①
,给出以下三个结论:① ;②
;② ;③
;③ ,其中正确结论的个数是( )
,其中正确结论的个数是( )
A. 0 B. 1 C. 2 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:我们知道,比较两数(式)大小有很多方法,“作差法”是常用的方法之一,其原理是不等式(或等式)的性质:若
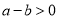 ,则
,则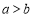 ;若
;若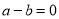 ,则
,则 ;若
;若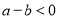 ,则
,则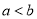 .
.例:已知
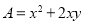 ,
,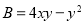 ,其中
,其中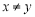 ,求证:
,求证: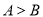 .
.证明:
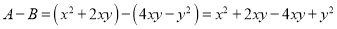
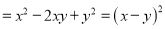 .
.∵
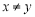 ,∴
,∴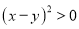 ,∴
,∴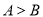 .
.(1)操作感知:比较大小:
①若
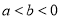 ,则
,则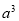 ______
______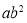 ;
;②
 ______
______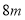 .
.(2)类比探究:已知
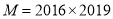 ,
,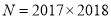 ,试运用上述方法比较
,试运用上述方法比较 、
、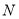 的大小,并说明理由.
的大小,并说明理由.(3)应用拓展:已知
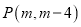 ,
, 为平面直角坐标系中的两点,小明认为,无论
为平面直角坐标系中的两点,小明认为,无论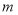 取何值,点
取何值,点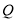 始终在点
始终在点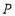 的上方,小明的猜想对吗?为什么?
的上方,小明的猜想对吗?为什么?
相关试题

