【题目】如图,△ABC 中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.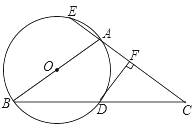
(1)求证:DF是⊙O的切线;
(2)若 ![]() ,半径OA=3,求AE的长.
,半径OA=3,求AE的长.
参考答案:
【答案】
(1)证明:连接OD,
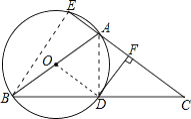
∵OB=OD,
∴∠B=∠ODB,
∵AB=AC,
∴∠B=∠C,
∴∠ODB=∠C,
∴OD∥AC,
∵DF⊥AC,
∴OD⊥DF,
∴DF是⊙O的切线
(2)解:连接BE,AD,∵AB是直径,
∴∠AEB=∠ADB=90°,
∵AB=AC,
∴∠ABC=∠C,BD=DC,
∵sinC= ![]() ,
,
∴sin∠ABC= ![]() ,
,
∵AB=2OA=6,
∴AD=2 ![]() ,
,
∴BD= ![]() ,
,
∴BC=2BD= ![]() ,
,
在Rt△BEC中,∵sinC= ![]() ,
,
∴BE= ![]() BC=
BC= ![]() ,
,
在Rt△ABE中,AE= ![]()
【解析】(1)要证切线可连接半径,证垂直,即证OD⊥DF即可;(2)出现直径时,连接BE,AD,构造出90度的圆周角,利用sinC的定义,求出BE,再利用勾股定理求出AE.
【考点精析】通过灵活运用切线的性质定理和切线的判定定理,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,它是一个长为2m,宽为2n的长方形,沿图中的虚线剪开均分成四个小长方形,然后按图(2)形状拼成一个正方形.
(1)你认为图(2)中的阴影部分的正方形边长为
(2)请用两种不同的方法表示图(2)阴影部分的面积;
方法一: 方法二:
(3)观察图(2),写出三个代数式:(m+n)2,(m﹣n)2,mn之间的等量关系.
(4)根据(3)题中的等量关系,解决下列问题:若a+b=7,ab=5,求(a﹣b)2的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:抛物线y=x2+(2m-1)x+m2-1经过坐标原点,且当x<0时,y随x的增大而减小.
(1)求抛物线的解析式;
(2)结合图象写出y<0时,对应的x的取值范围;
(3)设点A是该抛物线上位于x轴下方的一个动点,过点A作x轴的平行线交抛物线于另一点D,再作AB⊥x轴于点B,DC⊥x轴于点C.当BC=1时,直接写出矩形ABCD的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】石头剪子布,又称“猜丁壳”,是一种起源于中国流传多年的猜拳游戏.游戏时的各方每次用一只手做“石头”、“剪刀”、“布”三种手势中的一种,规定“石头”胜“剪刀”、“剪刀”胜“布”、“布”胜“石头” .两人游戏时,若出现相同手势,则不分胜负游戏继续,直到分出胜负,游戏结束.三人游戏时,若三种手势都相同或都不相同,则不分胜负游戏继续;若出现两人手势相同,则视为一种手势与第三人所出手势进行对决,此时,参照两人游戏规则.例如甲、乙二人同时出石头,丙出剪刀,则甲、乙获胜.假定甲、乙、丙三人每次都是随机地做这三种手势,那么:
(1)直接写出一次游戏中甲、乙两人出第一次手势时,不分胜负的概率;
(2)请你画出树状图求出一次游戏中甲、乙、丙三人出第一次手势时, 不分胜负的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)动手操作:
如图1所示,已知A、B、C三个点都在网格纸的格点上,∠1是∠ABC的余角,∠2是∠ABC的补角,CD⊥AB于点D,CE∥AB,试在图中分别画出:∠1、∠2、垂线段CD和直线CE.
(2)已知:如图2,点E在DF上,点B在AC上,∠1=∠2,∠C=∠D,试说明:AC∥DF,请将下面的解答过程补充完整:
解:∵∠1=∠2(已知)
又∵∠1=∠3
∴ = (等量代换)
∴EC∥DB
∴∠C= (两直线平行,同位角相等)
∵∠C=∠D(已知)
∴∠D=
∴AC∥DF

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(8,8),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.
(1)求证:△CBG≌△CDG;
(2)求∠HCG的度数;判断线段HG、OH、BG的数量关系,并说明理由;
(3)连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,四边形AEBD能否为矩形?如果能,请求出点H的坐标;如果不能,请说明理由.

-
科目: 来源: 题型:
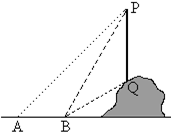
查看答案和解析>>【题目】如图所示,某数学活动小组要测量山坡上的电线杆PQ的高度.他们采取的方法是:先在地面上的点A处测得杆顶端点P的仰角是45°,再向前走到B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°,这时只需要测出AB的长度就能通过计算求出电线杆PQ的高度.你同意他们的测量方案吗?若同意,画出计算时的图形,简要写出计算的思路,不用求出具体值;若不同意,提出你的测量方案,并简要写出计算思路.
相关试题

