【题目】已知:抛物线y=x2+(2m-1)x+m2-1经过坐标原点,且当x<0时,y随x的增大而减小.
(1)求抛物线的解析式;
(2)结合图象写出y<0时,对应的x的取值范围;
(3)设点A是该抛物线上位于x轴下方的一个动点,过点A作x轴的平行线交抛物线于另一点D,再作AB⊥x轴于点B,DC⊥x轴于点C.当BC=1时,直接写出矩形ABCD的周长.
参考答案:
【答案】
(1)解:由y=x2+(2m-1)x+m2-1经过坐标原点,得
m2-1=0,解得m=1或m=-1.
当x<0时,y随x的增大而减小,
得m=-1.
抛物线的解析式y=x2-3x
(2)解:由图1,得

位于x轴下方的部分,
y<0时,对应的x的取值范围0<x<3
(3)解:如图2,

由AD∥x轴,得
A、D关于对称轴x=1.5对称,
B、C关于对称轴x=1.5对称,且BC=1,得1.5-0.5=1,即B(1,0).
当x=1时,y=1-3=-2,
即A(1,-2).
矩形ABCD的周长为2(AB+BC)=2×(2+1)=6
【解析】(1)由“当x<0时,y随x的增大而减小”可知m=1时,对称轴为x=-1,对称轴右侧有一部分y随x的增大而增大,不符合题意,舍去,取m=-1;(2)数形结合,x轴下方对应的x值;(3)数形结合,BC=1,再结合对称轴,分别求出A、D坐标,进而求出周长.
-
科目: 来源: 题型:
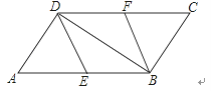
查看答案和解析>>【题目】如图,在ABCD中,E、F分别为边AB、CD的中点,连接DE、BF、BD.
(1)求证:△ADE≌△CBF
(2)当AD⊥BD时,请你判断四边形BFDE的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
在数学课上,老师提出如:下问题
尺规作图:过圆外一点作园的切线
已知:圆O和点P
求作:过点P的圆O的切线
小涵的主要作法如下:
如图:①连接OP,作线段OP的中点A
②以A为圆心,OA长为半径作圆,交圆O于点B,C
③作直线PB和PC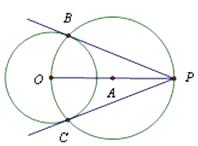
所以PB和PC就是所求的切线
老师说:“小涵的作法正确.”
请回答:小涵的作图依据是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,它是一个长为2m,宽为2n的长方形,沿图中的虚线剪开均分成四个小长方形,然后按图(2)形状拼成一个正方形.
(1)你认为图(2)中的阴影部分的正方形边长为
(2)请用两种不同的方法表示图(2)阴影部分的面积;
方法一: 方法二:
(3)观察图(2),写出三个代数式:(m+n)2,(m﹣n)2,mn之间的等量关系.
(4)根据(3)题中的等量关系,解决下列问题:若a+b=7,ab=5,求(a﹣b)2的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】石头剪子布,又称“猜丁壳”,是一种起源于中国流传多年的猜拳游戏.游戏时的各方每次用一只手做“石头”、“剪刀”、“布”三种手势中的一种,规定“石头”胜“剪刀”、“剪刀”胜“布”、“布”胜“石头” .两人游戏时,若出现相同手势,则不分胜负游戏继续,直到分出胜负,游戏结束.三人游戏时,若三种手势都相同或都不相同,则不分胜负游戏继续;若出现两人手势相同,则视为一种手势与第三人所出手势进行对决,此时,参照两人游戏规则.例如甲、乙二人同时出石头,丙出剪刀,则甲、乙获胜.假定甲、乙、丙三人每次都是随机地做这三种手势,那么:
(1)直接写出一次游戏中甲、乙两人出第一次手势时,不分胜负的概率;
(2)请你画出树状图求出一次游戏中甲、乙、丙三人出第一次手势时, 不分胜负的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC 中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.
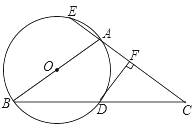
(1)求证:DF是⊙O的切线;
(2)若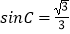 ,半径OA=3,求AE的长.
,半径OA=3,求AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)动手操作:
如图1所示,已知A、B、C三个点都在网格纸的格点上,∠1是∠ABC的余角,∠2是∠ABC的补角,CD⊥AB于点D,CE∥AB,试在图中分别画出:∠1、∠2、垂线段CD和直线CE.
(2)已知:如图2,点E在DF上,点B在AC上,∠1=∠2,∠C=∠D,试说明:AC∥DF,请将下面的解答过程补充完整:
解:∵∠1=∠2(已知)
又∵∠1=∠3
∴ = (等量代换)
∴EC∥DB
∴∠C= (两直线平行,同位角相等)
∵∠C=∠D(已知)
∴∠D=
∴AC∥DF

相关试题

