【题目】下列说法:①有一个角是![]() 的等腰三角形是等边三角形;②如果三角形的一个外角平分线平行三角形的一边,那么这个三角形是等腰三角形;③三角形三边的垂直平分线的交点与三角形三个顶点的距离相等;④有两个角相等的等腰三角形是等边三角形.其中正确的个数有( )
的等腰三角形是等边三角形;②如果三角形的一个外角平分线平行三角形的一边,那么这个三角形是等腰三角形;③三角形三边的垂直平分线的交点与三角形三个顶点的距离相等;④有两个角相等的等腰三角形是等边三角形.其中正确的个数有( )
A. ![]() 个B.
个B. ![]() 个C.
个C. ![]() 个D.
个D. ![]() 个
个
参考答案:
【答案】C
【解析】
根据等边三角形及等腰三角形的判定方法对各选项逐一判断即可.
当60°角是等腰三角形顶角时,两个底角为60°,三角形是等边三角形,
当60°角是底角时,顶角为60°,三角形是等边三角形,故①正确,
如图,BE为△ABC的外角平分线,且BE//AC,
∵BE//AC
∴∠A=∠EBD,∠C=∠CBE,
∵BE平分∠CBD,
∴∠CBE=∠EBD,
∴∠A=∠C,
∴AB=BC,
∴△ABC是等腰三角形,故②正确,

∵线段垂直平分线时的得到线段两端的距离相等,
∴三角形三边的垂直平分线的交点与三角形三个顶点的距离相等;故③正确,
∵等腰三角形的两个底角相等,不一定是60°,
∴有两个角相等的等腰三角形不一定是等边三角形,故④错误,
综上所述:正确的有①②③共3个,
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中, 的平分线相交于点D,
的平分线相交于点D, 过点D且
过点D且 ,分别交AB、AC于点E、F、AB=6,AC=10,则△AEF的周长__.
,分别交AB、AC于点E、F、AB=6,AC=10,则△AEF的周长__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长度为1个单位长度的小正方形组成的正方形网格纸中,点A、B、C在小正方形的顶点上.
(1)求
 的面积;
的面积;(2)在图中画出与
 关于直线1成轴对称的
关于直线1成轴对称的 ;
;(3)在如图所示网格纸中,以
 为一边作与
为一边作与 全等的三角形,可以作出多少个三角形与
全等的三角形,可以作出多少个三角形与 全等(不要超出网格纸的范围).
全等(不要超出网格纸的范围).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,画
 ,并画
,并画 的平分线
的平分线 .
.(1)将三角尺的直角顶点落在
 的任意一点P上,使三角尺的两条直角边与
的任意一点P上,使三角尺的两条直角边与 的两边分别垂直,垂足为E、F(如图1),则
的两边分别垂直,垂足为E、F(如图1),则
 (选填<,>,=)
(选填<,>,=)
(2)把三角尺绕着点P旋转(如图2),
 与
与 相等吗?试猜想
相等吗?试猜想 、
、 的大小关系,并说明理由.
的大小关系,并说明理由.拓展延伸1:在(2)条件下,过点P作直线
 ,分别交
,分别交 、
、 于点G、H,如图3
于点G、H,如图3①图中全等三角形有多少对(不添加辅助线)
②猜想
 、
、 、
、 之间的关系,并证明你的猜想.
之间的关系,并证明你的猜想.拓展延伸2:
画
 ,并画
,并画 的平分线
的平分线 ,在
,在 上任取一点P,作
上任取一点P,作 .
. 的两边分别与
的两边分别与 、
、 相交于E、F两点(如图4),
相交于E、F两点(如图4), 与
与 相等吗?请说明理由.
相等吗?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】为提高市民的环保意识,倡导“节能减排,绿色出行”,某市计划在城区投放一批“共享单车”这批单车分为A,B两种不同款型,其中A型车单价400元,B型车单价320元.
(1)今年年初,“共享单车”试点投放在某市中心城区正式启动.投放A,B两种款型的单车共100辆,总价值36800元.试问本次试点投放的A型车与B型车各多少辆?
(2)试点投放活动得到了广大市民的认可,该市决定将此项公益活动在整个城区全面铺开.按照试点投放中A,B两车型的数量比进行投放,且投资总价值不低于184万元.请问城区10万人口平均每100人至少享有A型车与B型车各多少辆?
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀剪下全等的四块小长方形,然后按图2拼成一个正方形.
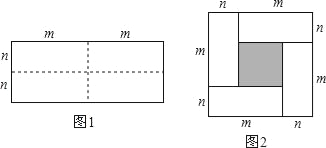
(1)直接写出图2中的阴影部分面积;
(2)观察图2,请直接写出下列三个代数式(m+n)2,(m﹣n)2,mn之间的等量关系;
(3)根据(2)中的等量关系,解决如下问题:若p+q=9,pq=7,求(p﹣q)2的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)
 的立方根是______________.
的立方根是______________.(2)已知某正数的两个平方根分别是a+3和2a-15,b的立方根是-2,则3a+b的算术平方根是___________.
相关试题

