【题目】如图,已知直线l1:y=-2x+4与x、y轴分别交于点N、C,与直线l2:y=kx+b(k≠0)交于点M,点M的横坐标为1,直线l2与x轴的交点为A(-2,0)
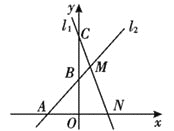
(1)求k,b的值;
(2)求四边形MNOB的面积.
参考答案:
【答案】(1)k= ![]() ,b=
,b= ![]() ;(2)
;(2)![]()
【解析】
(1)根据待定系数法可求出解析式,得到k、b的值;
(2)根据函数解析式与坐标轴的交点,可利用面积公式求出四边形的面积.
(1)M为l1与l2的交点
令M(1,y),代入y=2x+4中,解得y=2,
即M(1,2),
将M(1,2)代入y=kx+b,得k+b=2①
将A(-2,0)代入y=kx+b,得-2k+b=0②
由①②解得k=![]() ,b=
,b=![]()
(2)解:由(1)知l2:y=![]() x+
x+ ![]() ,当x=0时
,当x=0时
y= ![]() 即OB=
即OB=![]()
∴S△AOB=![]() OA·OB=
OA·OB= ![]() ×2×
×2×![]() =
=![]()
在y=-2x+4令y=0,得N(2,0)
又因为A(-2,0),故AN=4
所以S△AMN= ![]() ×AN×ym=
×AN×ym= ![]() ×4×2=4
×4×2=4
故SMNOB=S△AMN-S△AOB=4-![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】目前节能灯在各城市已基本普及,今年某市面向县级及农村地区推广,为响应号召,朝阳灯饰商场用了
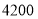 元购进甲型和乙型两种节能灯.这两种型号节能灯的进价、售价如表:
元购进甲型和乙型两种节能灯.这两种型号节能灯的进价、售价如表:进价(元/只)
售价(元/只)
甲型
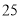
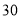
乙型
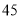
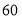
特别说明:毛利润=售价-进价;
(1)朝阳灯饰商场销售甲型节能灯一只毛利润是______元.
(2)如果朝阳灯饰商场购买甲,乙两种节能灯共
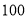 只,其中买了甲型节能灯多少只?
只,其中买了甲型节能灯多少只?(3)现在朝阳灯饰商场购进甲型节能灯
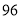 只,请你帮助商场计算一下销售完节能灯时所获的毛利润是多少?
只,请你帮助商场计算一下销售完节能灯时所获的毛利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将ABCD的AD边延长至点E,使DE=
 AD,连接CE,F是BC边的中点,连接FD.
AD,连接CE,F是BC边的中点,连接FD.(1)求证:四边形CEDF是平行四边形;
(2)若AB=3,AD=4,∠A=60°,求CE的长.

-
科目: 来源: 题型:
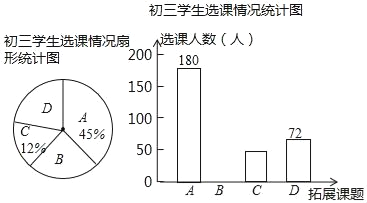
查看答案和解析>>【题目】某校实验课程改革,初三年级设罝了A,B,C,D四门不同的拓展性课程(每位学生只选修其中一门,所有学生都有一门选修课程),学校摸底调査了初三学生的选课意向,并将调查结果绘制成两个不完整的统计图,问该校初三年级共有多少学生?其中要选修B、C课程的各有多少学生?
-
科目: 来源: 题型:
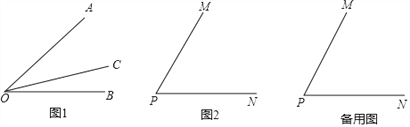
查看答案和解析>>【题目】【探索新知】:如图1,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”.
(1)一个角的平分线 这个角的“巧分线”;(填“是”或“不是”)
(2)如图2,若∠MPN=α,且射线PQ是∠MPN的“巧分线”,则∠MPQ= ;(用含α的代数式表示出所有可能的结果)
【深入研究】:如图2,若∠MPN=60°,且射线PQ绕点P从PN位置开始,以每秒10°的速度逆时针旋转,当PQ与PN成180°时停止旋转,旋转的时间为t秒.
(3)当t为何值时,射线PM是∠QPN的“巧分线”;
(4)若射线PM同时绕点P以每秒5°的速度逆时针旋转,并与PQ同时停止,请直接写出当射线PQ是∠MPN的“巧分线”时t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,二次函数y=x2+bx+c(b,c都是常数)的图象经过点(1,0)和(0,2).
(1)当﹣2≤x≤2时,求y的取值范围.
(2)已知点P(m,n)在该函数的图象上,且m+n=1,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列变形中:
①由方程
 =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;②由方程
 x=
x= 两边同除以
两边同除以 ,得x=1;
,得x=1;③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣
 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
相关试题

