【题目】小明和哥哥在环形跑道上练习长跑.他们从同一起点沿相反方向同时出发,每隔25秒钟相遇一次.现在,他们从同一起跑点沿相同方向同时出发,经过25分钟哥哥追上了小明,并且比小明多跑了20圈,求:
(1)哥哥速度是小明速度的多少倍?
(2)哥哥追上小明时,小明跑了多少圈?
参考答案:
【答案】(1)哥哥速度是小明速度的2倍;(2)20圈.
【解析】(1)由“他们从同一起点沿相反方向同时出发,每隔25秒钟相遇一次”得到等量关系:哥哥所跑路程+小明所跑路程=环形跑道的周长;由“经过25分钟哥哥追上小明,并且比小明多跑了20圈”,知经过![]() 分钟哥哥追上小明,并且比小明多跑了1圈,得到等量关系:哥哥所跑路程-小明所跑路程=环形跑道的周长,据此列出方程组,求出问题的解.
分钟哥哥追上小明,并且比小明多跑了1圈,得到等量关系:哥哥所跑路程-小明所跑路程=环形跑道的周长,据此列出方程组,求出问题的解.
(2)由(1)中求出的哥哥的速度与小明的速度的比为2:1,可知在时间相同时,他们所行的路程比也为2:1.如果设小明跑了x圈,那么哥哥跑了2x圈.根据哥哥比小明多跑了20圈列式解答即可.
解:设哥哥的速度是V1米/秒,小明的速度是V2米/秒.环形跑道的周长为s米.
(1)由题意,有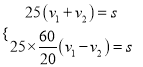 ,
,
整理得,4v2=2v1,
所以,V1=2V2.
答:哥哥速度是小明速度的2倍.
(2)设小明跑了x圈,那么哥哥跑了2x圈.
根据题意,得2x﹣x=20,
解得,x=20.
故经过了25分钟小明跑了20圈.
“点睛”本题考查分式方程、一元一次方程的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.本题要注意追及问题和相遇问题不同的求解方法及时间相同,路程比等于速度比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若△ABC中,∠A:∠B:∠C=2:3:4,则△ABC是 三角形.(填:锐角或直角或钝角)
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解居民用电情况,小陈在小区内随机抽查了30户家庭的月用电量,结果如下表:
月用电量/度
40
50
60
80
90
100
户数
6
7
9
5
2
1
则这30户家庭的月用电量的众数和中位数分别是 ( )
A. 60,60 B. 60,50 C. 50,60 D. 50,70
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的两边长分别为2、5,则三角形的周长为
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班数学活动小组的同学用纸板制作长方体包装盒,其平面展开图和相关尺寸如下,其中阴影部分为内部粘贴角料(单位:毫米).

(1)此长方体包装盒的体积为______立方毫米(用含x,y的式子表示).
(2)若内部粘贴角料的面积占长方体表面纸板面积的
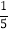 ,则当x=40,y=70时,制作这样一个长方体共需要纸板多少平方毫米?
,则当x=40,y=70时,制作这样一个长方体共需要纸板多少平方毫米? -
科目: 来源: 题型:
查看答案和解析>>【题目】如果等腰三角形的底角是50°,那么这个三角形的顶角的度数是
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的每一个内角为108°,则这个多边形是 边形,它的内角和是
相关试题

