【题目】在平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是(0,4)、(﹣1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.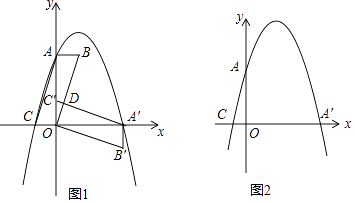
(1)若抛物线经过点C、A、A′,求此抛物线的解析式;
(2)点M时第一象限内抛物线上的一动点,问:当点M在何处时,△AMA′的面积最大?最大面积是多少?并求出此时M的坐标;
(3)若P为抛物线上一动点,N为x轴上的一动点,点Q坐标为(1,0),当P、N、B、Q构成平行四边形时,求点P的坐标,当这个平行四边形为矩形时,求点N的坐标.
参考答案:
【答案】
(1)
解:如图1中,
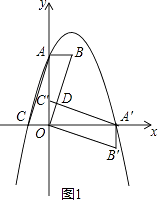
∵平行四边形ABOC绕点O顺时针旋转90°,得到平行四边
形A′B′OC′,点A的坐标是(0,4),
∴点A′的坐标为(4,0).
∵抛物线过点C,A,A′,设抛物线的函数解析式为
y=ax2+bx+c(a≠0)可得:
 ,解得:
,解得: 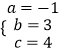 ,
,
∴抛物线的函数解析式为y=﹣x2+3x+4.
(2)
解:如图2中,连接AA′,设直线AA′的函数解析式为y=kx+b,
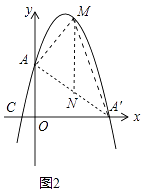
可得: ![]() ,解得:
,解得: ![]() ,
,
∴直线AA′的函数解析式是y=﹣x+4.
设M(x,﹣x2+3x+4),作MN∥y轴交AA′于N,则N(m,﹣m+4),
S△AMA′= ![]() ×4×[﹣x2+3x+4﹣(﹣x+4)]=﹣2(x﹣2)2+8,
×4×[﹣x2+3x+4﹣(﹣x+4)]=﹣2(x﹣2)2+8,
∵﹣2<0,
∴x=2时,△AMA′的面积最大,最大面积为8,
∴M(2,6).
(3)
解:如图3中,
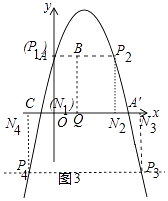
设P点的坐标为(x,﹣x2+3x+4),当P、N、B、Q构成平行四边形时,
①当BQ为边时,PN∥BQ 且PN=BQ,
∵BQ=4,
∴﹣x2+3x+4=±4.
当﹣x2+3x+4=4时,x=0或3,
可得P1(0,4),P2(3,4);
当﹣x2+3x+4=﹣4时,x= ![]() ,可得P3(
,可得P3( ![]() ,﹣4),P4(
,﹣4),P4( ![]() ,﹣4).
,﹣4).
②当BQ为对角线时,PB∥x轴,即P1,P2的坐标不变;
当这个平行四边形为矩形时,即P1(0,4),P2(3,4),N1(0,0),N2(3,0).
综上所述,当P1(0,4),P2(3,4),P3( ![]() ,﹣4),P4(
,﹣4),P4( ![]() ,﹣4).时,P、N、B、Q构成平行四边形;
,﹣4).时,P、N、B、Q构成平行四边形;
当这个平行四边形为矩形时,N1(0,0),N2(3,0).
【解析】(1)先确定C,A,A′三点坐标,利用待定系数法,转化为解方程组即可.(2)如图2中,连接AA′,设直线AA′的函数解析式为y=kx+b,设M(x,﹣x2+3x+4),作MN∥y轴交AA′于N,则N(m,﹣m+4),构建二次函数后利用二次函数的性质解决问题即可.(3)分两种情形讨论即可.①当BQ为边时,PN∥BQ 且PN=BQ,由BQ=4,可得﹣x2+3x+4=±4.解方程可以得到点P的横坐标.②当BQ为对角线时,PB∥x轴,即P1 , P2的坐标不变;当这个平行四边形为矩形时,点N的坐标利用图象即可解决.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明从点A出发,前进10m后向右转20°,再前进10m后又向右转20°,这样一直下去,直到他第一次回到出发点A为止,他所走的路径构成了一个多边形.
(1)小明一共走了多少米?
(2)这个多边形的内角和是多少度?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,∠B=90°,分别作其内角∠ACB与外角∠DAC的平分线,且两条角平分线所在的直线交于点E.
(1)∠E= °;
(2)分别作∠EAB与∠ECB的平分线,且两条角平分线交于点F.
①依题意在图1中补全图形;
②求∠AFC的度数;
(3)在(2)的条件下,射线FM在∠AFC的内部且∠AFM=
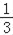 ∠AFC,设EC与AB的交点为H,射线HN在∠AHC的内部且∠AHN=
∠AFC,设EC与AB的交点为H,射线HN在∠AHC的内部且∠AHN=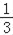 ∠AHC,射线HN与FM交于点P,若∠FAH,∠FPH和∠FCH满足的数量关系为∠FCH=m∠FAH+n∠FPH,请直接写出m,n的值.
∠AHC,射线HN与FM交于点P,若∠FAH,∠FPH和∠FCH满足的数量关系为∠FCH=m∠FAH+n∠FPH,请直接写出m,n的值.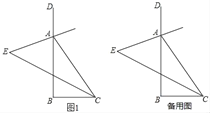
-
科目: 来源: 题型:
查看答案和解析>>【题目】现代互联网技术的广泛应用,催生了快递行业的高度发展,据调查,长沙市某家小型“大学生自主创业”的快递公司,今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件,现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递总件数的月平均增长率;
(2)如果平均每人每月最多可投递0.6万件,那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将⊙O沿弦AB折叠,圆弧恰好经过圆心O,点P是优弧
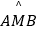 上一点,则∠APB的度数为( )
上一点,则∠APB的度数为( ) 
A.45°
B.30°
C.75°
D.60° -
科目: 来源: 题型:
查看答案和解析>>【题目】在同一坐标系中,一次函数y=ax+2与二次函数y=x2+a的图象可能是( )
A.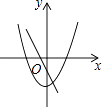
B.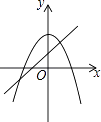
C.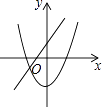
D.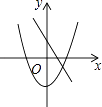
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:y=kx+4
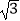 与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是( )
与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是( ) 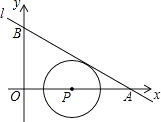
A.6
B.8
C.10
D.12
相关试题

