【题目】如图①,已知抛物线C1:y=a(x+1)2﹣4的顶点为C,与x轴相交于A、B两点(点A在点B的左边),点B的横坐标是1.
(1)求点C的坐标及a 的值;
(2)如图②,抛物线C2与C1关于x轴对称,将抛物线C2向右平移4个单位,得到抛物线C3 . C3与x轴交于点B、E,点P是直线CE上方抛物线C3上的一个动点,过点P作y轴的平行线,交CE于点F.
①求线段PF长的最大值;
②若PE=EF,求点P的坐标.
参考答案:
【答案】
(1)解:顶点C为(﹣1,﹣4).
∵点B(1,0)在抛物线C1上,∴0=a(1+1)2﹣4,解得,a=1;
(2)解:①∵C2与C1关于x轴对称,
∴抛物线C2的表达式为y=﹣(x+1)2+4,
抛物线C3由C2平移得到,
∴抛物线C3为y=﹣(x﹣3)2+4=﹣x2+6x﹣5,
∴E(5,0),
设直线CE的解析式为:y=kx+b,
则 ![]() ,
, 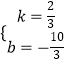 ,
,
∴直线CE的解析式为y= ![]() ,
,
设P(x,﹣x2+6x﹣5),则F(x, ![]() ),
),
∴PF=(﹣x2+6x﹣5)﹣( ![]() )=﹣x2+
)=﹣x2+ ![]() x﹣
x﹣ ![]() =﹣(x﹣
=﹣(x﹣ ![]() )2+
)2+ ![]() ,
,
∴当x= ![]() 时,PF有最大值为
时,PF有最大值为 ![]() ;
;
②若PE=EF,∵PF⊥x轴,
∴x轴平分PF,
∴﹣x2+6x﹣5=﹣ ![]() ,
,
解得x1= ![]() ,x2=5(舍去)
,x2=5(舍去)
∴P( ![]() ,
, ![]() ).
).
【解析】(1)由抛物线的顶点式得到顶点C的坐标;由点B(1,0)在抛物线上,求出a的值;(2)①由C2与C1关于x轴对称,得到抛物线C2的表达式,抛物线C3由C2平移得到,得到抛物线C3的解析式,得到E点的坐标,直线CE的解析式,求出PF的最大值;②若PE=EF,∵PF⊥x轴,得到x轴平分PF,求出P点的坐标;此题是综合题,难度较大,计算和解方程时需认真仔细.
-
科目: 来源: 题型:
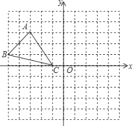
查看答案和解析>>【题目】如图,已知网格上最小的正方形的边长为1.
(1)分别写出A,B,C三点的坐标;
(2)作△ABC关于y轴的对称图形△A′B′C′(不写作法),想一想:关于y轴对称的两个点之间有什么关系?
(3)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方体的长为15宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )

A. 20 B. 25 C. 30 D. 32
-
科目: 来源: 题型:
查看答案和解析>>【题目】5月16日,我校进行了全校师生防灾减灾大演练,警报拉响后同学们匀速跑步到操场,在操场指定位置清点人数、听广播后,再沿原路匀速步行回教室,同学们离开教学楼的距离y与时间x的关系的大致图象是( )
A.
 B.
B.  C.
C.  D.
D. 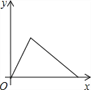
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:
①甲步行的速度为60米/分;
②乙走完全程用了32分钟;
③乙用16分钟追上甲;
④乙到达终点时,甲离终点还有300米
其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电信公司手机的A类收费标准如下:不管通话时间多长,每部手机每月必须缴月租费12元,另外,通话费按
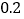 元
元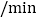 计;B类收费标准如下:没有月租费,但通话费按
计;B类收费标准如下:没有月租费,但通话费按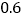 元
元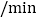 计
计 按照此类收费标准完成下列各题:
按照此类收费标准完成下列各题: 直接写出每月应缴费用
直接写出每月应缴费用 元
元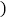 与通话时长
与通话时长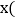 分
分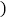 之间的关系式:
之间的关系式:A类:______B类:______
 若每月平均通话时长为300分钟,选择______类收费方式较少.
若每月平均通话时长为300分钟,选择______类收费方式较少. 求每月通话多长时间时,按
求每月通话多长时间时,按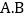 两类收费标准缴费,所缴话费相等.
两类收费标准缴费,所缴话费相等. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,利用标杆BE测量建筑物的高度,如果标杆BE长1.2m,测得AB=1.6m,BC=8.4m,楼高CD是多少?

相关试题

