【题目】如图,正方形ABCD边长为8cm,FG是等腰直角△EFG的斜边,FG=10cm,点B、F、C、G都在直线l上,△EFG以1cm/s的速度沿直线l向右做匀速运动,当t=0时,点G与B重合,记t(0≤t≤8)秒时,正方形与三角形重合部分的面积是Scm2 , 则S与t之间的函数关系图象大致为( )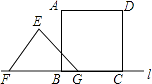
A.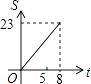
B.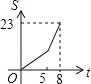
C.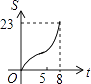
D.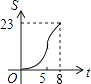
参考答案:
【答案】D
【解析】解:当0≤t≤5时,
设FG与AB交于点H,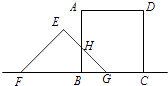
∴正方形与三角形重合部分的面积是△BHG的面积,
∴BG=t,
∵∠EGF=45°,
∴BH=BG=t,
∴S= ![]() BGBH=
BGBH= ![]() t2 ,
t2 ,
当5<t≤8时,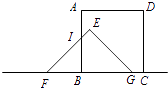
设EF与AB交于点I,
∴正方形与三角形重合部分的面积是四边形BIEG的面积,
∴BG=t,
∴FB=10﹣t,
∵∠EFG=45°,
∴FB=BI=10﹣t,
又∵△EFG的面积为: ![]() =25,
=25,
∴S=25﹣ ![]() FBBI=25﹣
FBBI=25﹣ ![]() (10﹣t)2=﹣
(10﹣t)2=﹣ ![]() t2+10t﹣25,
t2+10t﹣25,
故选(D)
【考点精析】通过灵活运用函数的图象,掌握函数的图像是由直角坐标系中的一系列点组成;图像上每一点坐标(x,y)代表了函数的一对对应值,他的横坐标x表示自变量的某个值,纵坐标y表示与它对应的函数值即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,填空:
(1)若∠4=∠3,则____∥_____,理由是______;
(2)若∠2=∠E,则____∥___,理由是____;
(3)若∠A=∠ABE=180°,则____∥___,理由是____;
(4)若∠2=∠____,则DA∥EB,理由是____;
(5)若∠DBC+∠_____=180°,则DB∥EC,理由是____;

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一内部装有水的直圆柱形水桶,桶高20公分;另有一直圆柱形的实心铁柱,柱高30公分,直立放置于水桶底面上,水桶内的水面高度为12公分,且水桶与铁柱的底面半径比为2:1.今小贤将铁柱移至水桶外部,过程中水桶内的水量未改变,若不计水桶厚度,则水桶内的水面高度变为多少公分?( )

A.4.5
B.6
C.8
D.9 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB∥CD,∠1=∠2,∠3=∠4.
(1)求证:AD∥BE;
(2)若∠B=∠3=2∠2,求∠D的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:EF⊥AC,垂足为点F,DM⊥AC,垂足为点M,DM的延长线交AB于点B,且∠1=∠C,点N在AD上,且∠2=∠3,试说明AB∥MN.
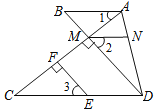
-
科目: 来源: 题型:
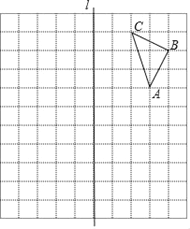
查看答案和解析>>【题目】如图,直线l与△ABC在边长为1个单位长度的小正方形网格中,点A,B,C都为网格线的交点.
(1)请画出△ABC关于直线l对称的△A1B1C1(点A,B,C的对称点分别为A1,B1,C1).
(2)请画出将线段AC向左平移3个单位,再向下平移5个单位得到的线段A2C2(点A,C的对应点分别为A2,C2),再以A2C2为斜边画一个等腰直角三角形A2B2C2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.
(1)AE与FC会平行吗?说明理由.
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么.

相关试题

