搜索
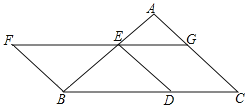
【题目】如图，以BC为底边的等腰
，点D，E，G分别在BC，AB，AC上，且
，
，延长GE至点F，使得
．
求证：四边形BDEF为平行四边形；
当
，
时，联结DF，求线段DF的长．
参考答案：
【答案】
证明见解析
D，F两点间的距离为
．
【解析】
由等腰三角形的性质得出
，证出
，四边形CDEG是平行四边形，得出
，证出
，得出
，即可得出结论；
证出
、
是等腰直角三角形，由勾股定理得出
，作
于M，连接DF，则
是等腰直角三角形，由勾股定理得出
，得出
，在
中，由勾股定理求出DF即可．
证明：
是等腰三角形，
，
，
，
，四边形CDEG是平行四边形，
，
，
，
，
，
四边形BDEF为平行四边形；
解：
，
，
、是等腰直角三角形，
，
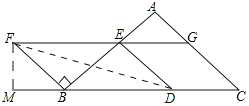
作于M，连接DF，如图所示：
则是等腰直角三角形，
，
，
在中，由勾股定理得：
，
即D，F两点间的距离为．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠ABC=90°，D是边AC上的一点，连接BD，使∠A=2∠1，E是BC上的一点，以BE为直径的⊙O经过点D．
（1）求证：AC是⊙O的切线；
（2）若∠A=60°，⊙O的半径为2，求阴影部分的面积．（结果保留根号和π） -
科目： 来源： 题型：
查看答案和解析>>【题目】某厂家生产的一种新型节能灯，为了打开市场出台了相关政策：由厂家协调，厂家按成本价提供产品给经营户自主销售，成本价与出厂价之间的差价由厂家承担．李明按照相关政策投资销售本产品．已知这种节能灯的成本价为每件10元，出厂价为每件12元，每月销售量y（件）与销售单价x（元）之间的关系近似满足一次函数：y=﹣10x+500．
（1）李明在开始销售的第一个月将销售单价定为20元，那么厂家这个月为他承担的总差价为多少元？
（2）设李明获得的利润为w（元），当销售单价定为多少元时，每月可获得最大利润？
（3）物价部门规定，这种节能灯的销售单价不得高于25元．如果李明想要每月获得的利润不低于3000元，那么厂家为他承担的总差价最少为多少元？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，ABCD中，
，点P按
方向运动，到达点B时运动停止，运动开始时以每秒2个长度单位匀速运动，到达D点后，改为每秒m个单位匀速运动，到达C后，改为每秒n个单位匀速运动，在整个运动过程中，
的面积S与运动时间t的函数关系如图所示．
求：
求AB、BC的长；
求m，n的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=ax2+b与x轴交于点A、B，且A点的坐标为（1，0），与y轴交于点C（0，1）．
（1）求抛物线的解析式，并求出点B坐标；
（2）过点B作BD∥CA交抛物线于点D，连接BC、CA、AD，求四边形ABCD的周长；（结果保留根号）
（3）在x轴上方的抛物线上是否存在点P，过点P作PE垂直于x轴，垂足为点E，使以B、P、E为顶点的三角形与△CBD相似？若存在请求出P点的坐标；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】实验室里，水平桌面上有甲、乙、丙三个圆柱形容器（容器足够高），底面半径之比为1：2：1，，用两个相同的管子在容器的5cm高度处连通（即管子底端离容器底5cm），现三个容器中，只有甲中有水，水位高1cm，如图所示．若每分钟同时向乙和丙注入相同量的水，开始注水1分钟，乙的水位上升
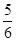cm，则开始注入 分钟的水量后，甲与乙的水位高度之差是0．5cm．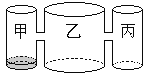
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在正方形ABCD中，点E是AD上的点，点F是BC的延长线上一点，CF=DE，连结BE和EF，EF与CD交于点G，且∠FBE=∠FEB．
（1）过点F作FH⊥BE于点H，证明：
= 
；
（2）猜想：BE、AE、EF之间的数量关系，并证明你的结论；
（3）若DG=2，求AE值．
相关试题
