Question

【题目】如图，在△ABC中，∠ACB＝90°，D是BC延长线上一点，E是BD垂直平分线与AB的交点，DE交AC于点F.求证：点E在AF的垂直平分线上．

Answer 1

【答案】见解析

【解析】试题分析：过E作EG垂直于AC，交AC于G，可得出EG∥BD故∠AEG=∠B，∠D=∠DEG．再根据E是BD的垂直平分线与AB的交点可得出∠B=∠D，根据ASA定理得出△AEG≌△FEG，进而可得出结论．

试题解析：

证明：如图所示：

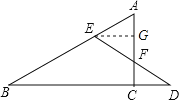
过E作EG垂直于AC，交AC于G，

∵∠ACB=90°，
∴EG∥BD，
∴∠AEG=∠B，∠D=∠DEG．
∵E是BD的垂直平分线与AB的交点，
∴BE=DE，
∴∠B=∠D，
∴∠AEG=∠DEG．
在△AEG与△FEG中，

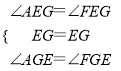
∴△AEG≌△FEG（ASA），
∴EA=EF．

又∵EG垂直于AC，

∴EG是AC的垂直平分线，

∴点E在AF的垂直平分线上．