【题目】湖州某企业新增了一个化工项目,为了节约资源,保护环境,该企业决定购买A、B两种型号的污水处理设备共10台,具体情况如下表:
A型 | B型 | |
价格(万元/台) | 15 | 12 |
月污水处理能力(吨/月) | 250 | 200 |
经预算,企业最多支出136万元购买设备,且要求月处理污水能力不低于2150吨.
(1)该企业有哪几种购买方案?
(2)哪种方案更省钱?并说明理由.
参考答案:
【答案】(1)有3种购买方案:第一种是购买3台A型污水处理设备,7台B型污水处理设备;第二种是购买4台A型污水处理设备,6台B型污水处理设备;第三种是购买5台A型污水处理设备,5台B型污水处理设备;(2)购买3台A型污水处理设备,7台B型污水处理设备更省钱.
【解析】
(1)设购买A型号的污水处理设备x台,则购买B型号的污水处理设备(10-x)台,根据购买资金不超过136万元及月处理污水能力不低于2150吨,即可得出关于x的一元一次不等式组,解之即可得出x的取值范围,再由x为整数即可得出各购买方案;
(2)根据总价=单价×数量,分别求出3种购买方案所需总费用,比较后即可得出结论.
(1)设购买![]() 型号的污水处理设备
型号的污水处理设备![]() 台,则购买
台,则购买![]() 型号的污水处理设备
型号的污水处理设备![]() 台,
台,
根据题意得:![]()
解得:![]()
∵![]() 是整数
是整数
∴![]() 或
或![]() 或
或![]() ,
,
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
答:有3种购买方案:第一种是购买3台A型污水处理设备,7台B型污水处理设备;第二种是购买4台A型污水处理设备,6台B型污水处理设备;第三种是购买5台A型污水处理设备,5台B型污水处理设备.
(2)当![]() 时,购买资金为15×3+12×7=129(万元),
时,购买资金为15×3+12×7=129(万元),
当![]() 时,购买资金为15×4+12×6=132(万元),
时,购买资金为15×4+12×6=132(万元),
当![]() 时,购买资金为15×5+12×5=135(万元).
时,购买资金为15×5+12×5=135(万元).
∵135>132>129,
∴为了节约资金,应购污水处理设备A型号3台,B型号7台.
答:购买3台A型污水处理设备,7台B型污水处理设备更省钱
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:ΔABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
(材料)如图,对任意符合条件的直角三角形BAC,绕其锐角顶点逆时针旋转90°得△DAE,所以∠BAE=90°,且四边形ACFD是一个正方形,它的面积和四边形ABFE面积相等,而四边形ABFE面积等于Rt△BAE和Rt△BFE的面积之和,根据图形我们就能证明勾股定理:
 .
.
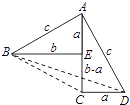
(请回答)如图是任意符合条件的两个全等的Rt△BEA和Rt△ACD拼成的,你能根据图示再写一种证明勾股定理的方法吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=BC,点D在AB的延长线上.
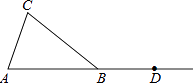
(1)利用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法). ①作∠CBD的平分线BM;
②作边BC上的中线AE,并延长AE交BM于点F.
(2)由(1)得:BF与边AC的位置关系是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC中,BE平分∠ABC交AC边于点E,过点E作DE∥BC交AB于点D,
(1)求证:△BDE为等腰三角形;
(2)若点D为AB中点,AB=6,求线段BC的长;
(3)在图2条件下,若∠BAC=60°,动点P从点B出发,以每秒1个单位的速度沿射线BE运动,请直接写出图3当△ABP为等腰三角形时t的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直线AB与x轴交于点A,与y轴交于点C(0,2),且与反比例函数y=﹣
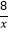 的图象在第二象限内交于点B,过点B作BD⊥x轴于点D,OD=2.
的图象在第二象限内交于点B,过点B作BD⊥x轴于点D,OD=2. 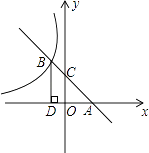
(1)求直线AB的解析式;
(2)若点P是线段BD上一点,且△PBC的面积等于3,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校举行“社会主义核心价值观”知识比赛活动,全体学生都参加比赛,学校对参赛学生均给与表彰,并设置一、二、三等奖和纪念奖共四个奖项,赛后将获奖情况绘制成如下所示的两幅不完整的统计图,请根据图中所给的信息,解答下列问题:

(1)该校共有名学生;
(2)在图①中,“三等奖”所对应扇形的圆心角度数是;
(3)将图②补充完整;
(4)从该校参加本次比赛活动的学生中随机抽查一名.求抽到获得一等奖的学生的概率.
相关试题

