搜索
【题目】如图，在△ABC中，AB=BC，点D在AB的延长线上．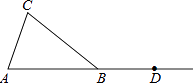 
（1）利用尺规按下列要求作图，并在图中标明相应的字母（保留作图痕迹，不写作法）． ①作∠CBD的平分线BM；
②作边BC上的中线AE，并延长AE交BM于点F．
（2）由（1）得：BF与边AC的位置关系是 ．
参考答案：
【答案】
（1）解：①如图所示：BM即为所求；
②如图所示：AF即为所求
（2）BF∥AC
【解析】解：（2）∵AB=BC， ∴∠CAB=∠C，
∵∠C+∠CAB=∠CBD，∠CBM=∠MBD，
∴∠C=∠CBM，
∴BF∥AC．
【考点精析】利用三角形的外角和等腰三角形的性质对题目进行判断即可得到答案，需要熟知三角形一边与另一边的延长线组成的角，叫三角形的外角；三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角；等腰三角形的两个底角相等（简称：等边对等角）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算下列各题
（1）计算：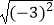
﹣（ 
）﹣1+（π﹣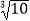 
）0﹣（﹣1）100；
（2）已知|a+1|+（b﹣3）2=0，求代数式（
﹣ 
）÷ 
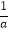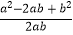的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点A、D、C、F在同一条直线上，AD=CF，AB=DE，BC=EF.
(1)求证：ΔABC≌△DEF；
(2)若∠A=55°，∠B=88°，求∠F的度数.
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下列材料：
（材料）如图，对任意符合条件的直角三角形BAC，绕其锐角顶点逆时针旋转90°得△DAE，所以∠BAE=90°，且四边形ACFD是一个正方形，它的面积和四边形ABFE面积相等，而四边形ABFE面积等于Rt△BAE和Rt△BFE的面积之和，根据图形我们就能证明勾股定理：
.
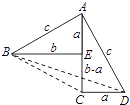
（请回答）如图是任意符合条件的两个全等的Rt△BEA和Rt△ACD拼成的，你能根据图示再写一种证明勾股定理的方法吗？
-
科目： 来源： 题型：
查看答案和解析>>【题目】湖州某企业新增了一个化工项目，为了节约资源，保护环境，该企业决定购买A、B两种型号的污水处理设备共10台，具体情况如下表：
A型
B型
价格（万元/台）
15
12
月污水处理能力（吨/月）
250
200
经预算，企业最多支出136万元购买设备，且要求月处理污水能力不低于2150吨．
（1）该企业有哪几种购买方案？
（2）哪种方案更省钱？并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，△ABC中，BE平分∠ABC交AC边于点E，过点E作DE∥BC交AB于点D，
（1）求证：△BDE为等腰三角形；
（2）若点D为AB中点，AB=6，求线段BC的长；
（3）在图2条件下，若∠BAC=60°，动点P从点B出发，以每秒1个单位的速度沿射线BE运动，请直接写出图3当△ABP为等腰三角形时t的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，直线AB与x轴交于点A，与y轴交于点C（0，2），且与反比例函数y=﹣
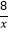的图象在第二象限内交于点B，过点B作BD⊥x轴于点D，OD=2．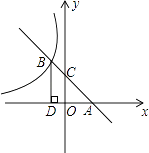 
（1）求直线AB的解析式；
（2）若点P是线段BD上一点，且△PBC的面积等于3，求点P的坐标．
相关试题
