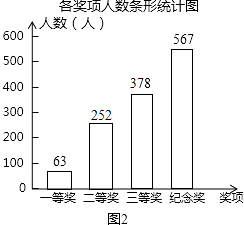
【题目】某学校举行“社会主义核心价值观”知识比赛活动,全体学生都参加比赛,学校对参赛学生均给与表彰,并设置一、二、三等奖和纪念奖共四个奖项,赛后将获奖情况绘制成如下所示的两幅不完整的统计图,请根据图中所给的信息,解答下列问题: 
(1)该校共有名学生;
(2)在图①中,“三等奖”所对应扇形的圆心角度数是;
(3)将图②补充完整;
(4)从该校参加本次比赛活动的学生中随机抽查一名.求抽到获得一等奖的学生的概率.
参考答案:
【答案】
(1)1260
(2)108°
(3)解:三等奖的人数为:1260×(1﹣20%﹣5%﹣45%)=378人,如图2,
(4)解:抽到获得一等奖的学生的概率为:63÷1260=5%
【解析】解:(1)该校共有学生数为:252÷20%=1260(名), 故答案为:1260.(2)一等奖扇形对应的百分比为:63÷1260=5%,
所以三等奖扇形对应的圆心角为:(1﹣20%﹣5%﹣45%)×360°=108°,
故答案为:108°.
(1)用二等奖的人数除以对应的百分比求出该校共有学生数,(2)先求出一等奖扇形对应的百分比,再求三等奖扇形对应的圆心角为:(1﹣20%﹣5%﹣45%)×360°=108°,(3)求出三等奖的人数再画出条形统计图,(4)用一等奖的学生数除以总人数就是抽到一等奖的概率,
-
科目: 来源: 题型:
查看答案和解析>>【题目】湖州某企业新增了一个化工项目,为了节约资源,保护环境,该企业决定购买A、B两种型号的污水处理设备共10台,具体情况如下表:
A型
B型
价格(万元/台)
15
12
月污水处理能力(吨/月)
250
200
经预算,企业最多支出136万元购买设备,且要求月处理污水能力不低于2150吨.
(1)该企业有哪几种购买方案?
(2)哪种方案更省钱?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC中,BE平分∠ABC交AC边于点E,过点E作DE∥BC交AB于点D,
(1)求证:△BDE为等腰三角形;
(2)若点D为AB中点,AB=6,求线段BC的长;
(3)在图2条件下,若∠BAC=60°,动点P从点B出发,以每秒1个单位的速度沿射线BE运动,请直接写出图3当△ABP为等腰三角形时t的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直线AB与x轴交于点A,与y轴交于点C(0,2),且与反比例函数y=﹣
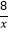 的图象在第二象限内交于点B,过点B作BD⊥x轴于点D,OD=2.
的图象在第二象限内交于点B,过点B作BD⊥x轴于点D,OD=2. 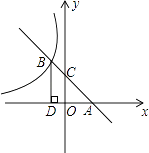
(1)求直线AB的解析式;
(2)若点P是线段BD上一点,且△PBC的面积等于3,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点E是对角线AC上一点,且CE=CD,过点E作EF⊥AC交AD于点F,连接BE.
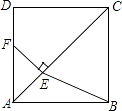
(1)求证:DF=AE;
(2)当AB=2时,求BE2的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直线L上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1、2、3,正放置的四个正方形的面积依次是S1、S2、S3、S4 , 则S1+2S2+2S3+S4=()
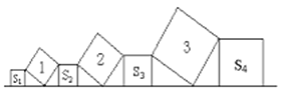
A. 5 B. 4 C. 6 D. 10
-
科目: 来源: 题型:
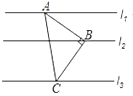
查看答案和解析>>【题目】如图,Rt△ABC中,∠ABC=90°,AB=BC,直线l1、l2、l3分别通过A、B、C三点,且l1∥l2∥l3.若l1与l2的距离为4,l2与l3的距离为6,则Rt△ABC的面积为___________.
相关试题

