搜索
【题目】如图，正比例函数y＝x与反比例函数y＝ 
的图像交于点A、点C，AB⊥x轴于点B，CD⊥x轴于点D，则四边形ABCD的面积为 ．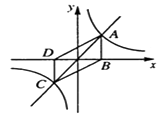 
参考答案：
【答案】2
【解析】因为直线 y=x与反比例函数
都关于原点对称，
所以OB=OD，OA=OC，
即四边形ABCD是平行四边形.
可设A（x,
）,
则SABCD=4S△OAB=4×
×x×=2.
所以答案是2.
【考点精析】解答此题的关键在于理解比例系数k的几何意义的相关知识，掌握几何意义：表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积，以及对平行四边形的判定的理解，了解两组对边分别平行的四边形是平行四边形：两组对边分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形；两组对角分别相等的四边形是平行四边形；对角线互相平分的四边形是平行四边形．
-
科目： 来源： 题型：
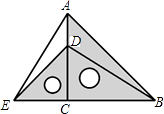
查看答案和解析>>【题目】把两个含有45°角的直角三角板如图放置，点D在AC上，连接AE、BD，试判断AE与BD的关系，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知直线y=﹣x+4与两坐标轴分别相交于点A，B两点，点C是线段AB上任意一点，过C分别作CD⊥x轴于点D，CE⊥y轴于点E．双曲线
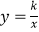与CD，CE分别交于点P，Q两点，若四边形ODCE为正方形，且 
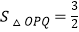，则k的值是（ ）
A.4
B.2
C.
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点P、Q是反比例函数y=
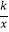图像上的两点，PA⊥y轴于点A，QN⊥x轴于点N，作PM⊥x轴于点M，QB⊥y轴于点B，连接PB、QM，△ABP的面积记为S1 ， △QMN的面积记为S2 ， 则S1S2 ． （填“＞”或“＜”或“=”） 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知在△ABC中，∠1=∠2．
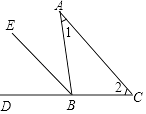
（1）请你添加一个与直线AC有关的条件，由此可得出BE是△ABC的外角平分线；
（2）请你添加一个与∠1有关的条件，由此可得出BE是△ABC的外角平分线；
（3）如果“已知在△ABC中，∠1=∠2不变”，请你把（1）中添加的条件与所得结论互换，所得的命题是否是真命题，理由是什么？ -
科目： 来源： 题型：
查看答案和解析>>【题目】在ABCD中，AD=8，AE平分∠BAD交BC于点E，DF平分∠ADC交BC于点F，且EF=2，则AB的长为（ ）
A．3 B．5 C．2或3 D．3或5
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了响应“中小学生每天锻炼1小时”的号召，某校开展了形式多样的“阳光体育”活动，小明对某班同学 参加锻炼的情况进行了调查与统计，并绘制了下面的图1与图2．
根据你对图1与图2的理解，回答下列问题：
（1）小明调查的这个班级有名学生．
（2）请你将图1中“乒乓球”部分补充完整．
（3）若这个学校共有1200名学生，估计参加乒乓球活动的学生有名学生．
（4）求出扇形统计图中表示“足球”的扇形的圆心角的度数．
相关试题
