【题目】把两个含有45°角的直角三角板如图放置,点D在AC上,连接AE、BD,试判断AE与BD的关系,并说明理由.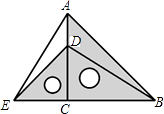
参考答案:
【答案】解:BF⊥AE,理由如下:
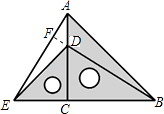
由题意可知:△ECD和△BCA都是等腰Rt△,
∴EC=DC,AC=BC,∠ECD=∠BCA=90°,
在△AEC和△BDC中
EC=DC,∠ECA=∠DCB,AC=BC,
∴△AEC≌△BDC(SAS).
∴∠EAC=∠DBC,AE=BD,
∵∠DBC+∠CDB=90°,∠FDA=∠CDB,
∴∠EAC+∠FDA=90°.
∴∠AFD=90°,即BF⊥AE.
故可得AE⊥BD且AE=BD.
【解析】先观察两条线短的位置关系,当两线段不相交时,可延长构造出三角形,由全等证出对应角相等,转化得到∠EAC+∠FDA=90°,进而证出结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算2a3a的结果等于
-
科目: 来源: 题型:
查看答案和解析>>【题目】星期天,玲玲骑自行车到郊外游玩,她离家的距离与时间的关系如图所示,请根据图象回答下列问题.

(1)玲玲到达离家最远的地方是什么时间?离家多远?
(2)她何时开始第一次休息?休息了多长时间?
(3)她骑车速度最快是在什么时候?车速多少?
(4)玲玲全程骑车的平均速度是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】菱形的一个内角是60°,边长为8 cm,则这个菱形较短的对角线长是______cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=﹣x+4与两坐标轴分别相交于点A,B两点,点C是线段AB上任意一点,过C分别作CD⊥x轴于点D,CE⊥y轴于点E.双曲线
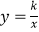 与CD,CE分别交于点P,Q两点,若四边形ODCE为正方形,且
与CD,CE分别交于点P,Q两点,若四边形ODCE为正方形,且 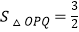 ,则k的值是( )
,则k的值是( )
A.4
B.2
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P、Q是反比例函数y=
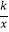 图像上的两点,PA⊥y轴于点A,QN⊥x轴于点N,作PM⊥x轴于点M,QB⊥y轴于点B,连接PB、QM,△ABP的面积记为S1 , △QMN的面积记为S2 , 则S1S2 . (填“>”或“<”或“=”)
图像上的两点,PA⊥y轴于点A,QN⊥x轴于点N,作PM⊥x轴于点M,QB⊥y轴于点B,连接PB、QM,△ABP的面积记为S1 , △QMN的面积记为S2 , 则S1S2 . (填“>”或“<”或“=”) 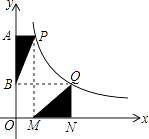
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正比例函数y=x与反比例函数y=
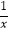 的图像交于点A、点C,AB⊥x轴于点B,CD⊥x轴于点D,则四边形ABCD的面积为 .
的图像交于点A、点C,AB⊥x轴于点B,CD⊥x轴于点D,则四边形ABCD的面积为 . 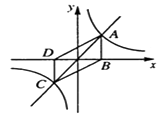
相关试题

