【题目】如图,已知在△ABC中,∠1=∠2.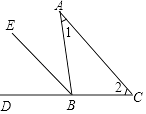
(1)请你添加一个与直线AC有关的条件,由此可得出BE是△ABC的外角平分线;
(2)请你添加一个与∠1有关的条件,由此可得出BE是△ABC的外角平分线;
(3)如果“已知在△ABC中,∠1=∠2不变”,请你把(1)中添加的条件与所得结论互换,所得的命题是否是真命题,理由是什么?
参考答案:
【答案】
(1)解:AC∥BE;
(2)解:∠1=∠ABE或∠1=∠DBE
(3)解:是真命题,理由如下:
∵BE是△ABC的外角平分线,
∴∠ABE=∠DBE,
又∵∠ABD是三角形ABC的外角,
∴∠ABD=∠1+∠2,
即∠ABE+∠DBE=∠1+∠2,
又∵∠ABE=∠DBE,∠1=∠2,
∴∠ABE=∠1,
∴AC∥BE.
【解析】①②要使BE是△ABC的外角平分线,结合三角形的外角的性质∠ABD=∠1+∠2,∠ABE=∠DBE,∠1=∠2,即证明∠ABE=∠1=∠DBE=∠2,进一步可得BE∥AC;
③根据平行线的性质和三角形的外角的性质即可证明。
本题综合运用了角平分线定义、平行线的性质和三角形的外角的性质。
【考点精析】本题主要考查了命题与定理的相关知识点,需要掌握我们把题设、结论正好相反的两个命题叫做互逆命题.如果把其中一个叫做原命题,那么另一个叫做它的逆命题;经过证明被确认正确的命题叫做定理才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=﹣x+4与两坐标轴分别相交于点A,B两点,点C是线段AB上任意一点,过C分别作CD⊥x轴于点D,CE⊥y轴于点E.双曲线
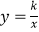 与CD,CE分别交于点P,Q两点,若四边形ODCE为正方形,且
与CD,CE分别交于点P,Q两点,若四边形ODCE为正方形,且 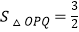 ,则k的值是( )
,则k的值是( )
A.4
B.2
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P、Q是反比例函数y=
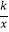 图像上的两点,PA⊥y轴于点A,QN⊥x轴于点N,作PM⊥x轴于点M,QB⊥y轴于点B,连接PB、QM,△ABP的面积记为S1 , △QMN的面积记为S2 , 则S1S2 . (填“>”或“<”或“=”)
图像上的两点,PA⊥y轴于点A,QN⊥x轴于点N,作PM⊥x轴于点M,QB⊥y轴于点B,连接PB、QM,△ABP的面积记为S1 , △QMN的面积记为S2 , 则S1S2 . (填“>”或“<”或“=”) 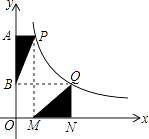
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正比例函数y=x与反比例函数y=
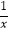 的图像交于点A、点C,AB⊥x轴于点B,CD⊥x轴于点D,则四边形ABCD的面积为 .
的图像交于点A、点C,AB⊥x轴于点B,CD⊥x轴于点D,则四边形ABCD的面积为 . 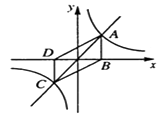
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,AD=8,AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,且EF=2,则AB的长为( )
A.3 B.5 C.2或3 D.3或5
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了响应“中小学生每天锻炼1小时”的号召,某校开展了形式多样的“阳光体育”活动,小明对某班同学 参加锻炼的情况进行了调查与统计,并绘制了下面的图1与图2.

根据你对图1与图2的理解,回答下列问题:
(1)小明调查的这个班级有名学生.
(2)请你将图1中“乒乓球”部分补充完整.
(3)若这个学校共有1200名学生,估计参加乒乓球活动的学生有名学生.
(4)求出扇形统计图中表示“足球”的扇形的圆心角的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知平行四边形ABCD的顶点A在第三象限,对角线AC的中点在坐标原点,一边AB与x轴平行且AB=2,若点A的坐标为(a,b),则点D的坐标为 .
相关试题

