【题目】如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF,则下列结论::①△EBF≌△DFC;②四边形AEFD为平行四边形;③当AB=AC,∠BAC=120°时,四边形AEFD是正方形.其中正确的结论是 . (请写出正确结论的序号).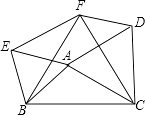
参考答案:
【答案】①②
【解析】解:∵△ABE、△BCF为等边三角形,
∴AB=BE=AE,BC=CF=FB,∠ABE=∠CBF=60°,
∴∠ABE﹣∠ABF=∠FBC﹣∠ABF,即∠CBA=∠FBE,
在△ABC和△EBF中,
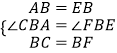 ,
,
∴△ABC≌△EBF(SAS),
∴EF=AC,
又∵△ADC为等边三角形,
∴CD=AD=AC,
∴EF=AD=DC,
同理可得△ABC≌△DFC,
∴DF=AB=AE=DF,
∴四边形AEFD是平行四边形,选项②正确;
∴∠FEA=∠ADF,
∴∠FEA+∠AEB=∠ADF+∠ADC,即∠FEB=∠CDF,
在△FEB和△CDF中,
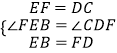 .
.
∴△FEB≌△CDF(SAS),选项①正确;
若AB=AC,∠BAC=120°,则有AE=AD,∠EAD=120°,此时AEFD为菱形,选项③错误,
所以答案是:①②.
【考点精析】认真审题,首先需要了解等边三角形的性质(等边三角形的三个角都相等并且每个角都是60°),还要掌握平行四边形的判定(两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】己知:如图,E、F分别是ABCD的AD、BC边上的点,且AE=CF.
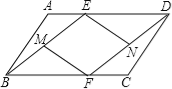
(1)求证:△ABE≌△CDF;
(2)若M、N分别是BE、DF的中点,连接MF、EN,试判断四边形MFNE是怎样的四边形,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明的妈妈在菜市场买回3斤萝卜、2斤排骨,准备做萝卜排骨汤.
妈妈:“今天买这两样菜共花了45元,上月买同重量的这两样菜只要36元”;
爸爸:“报纸上说了萝卜的单价上涨50%,排骨单价上涨20%”;
小明:“爸爸、妈妈,我想知道今天买的萝卜和排骨的单价分别是多少?”
请你通过列方程(组)求解这天萝卜、排骨的单价(单位:元/斤).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A、C分别在x轴上、y轴上,CB//OA,OA=8,若点B的坐标为(a,b),且b=
 .
.(1)直接写出点A、B、C的坐标;
(2)若动点P从原点O出发沿x轴以每秒2个单位长度的速度向右运动,当直线PC把四边形OABC分成面积相等的两部分停止运动,求P点运动时间;
(3)在(2)的条件下,在y轴上是否存在一点Q,连接PQ,使三角形CPQ的面积与四边形OABC的面积相等?若存在,求点Q的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一只蚂蚁沿着棱长为2的正方体表面从点A出发,经过3个面爬到点,如运动的路径是最短的,则AC的长为
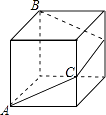
-
科目: 来源: 题型:
查看答案和解析>>【题目】亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某市初中学生每天进行体育锻炼的时间情况,随机抽样调查了100名涌中学生,根据调查结果得到如图所示的统计图表.
类别
时间t(小时)
人数
A
t≤0.5
5
B
0.5<t≤1
20
C
1<t≤1.5
a
D
1.5<t≤2
30
E
t>2
10
请根据图表信息解答下列问题:
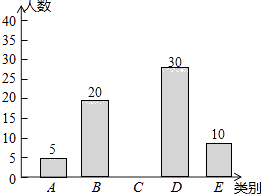
(1)a=;
(2)补全条形统计图;
(3)据了解该市大约有30万名初中学生,请估计该市初中学生每天进行体育锻炼时间在1小时以上的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E、F分别是AB、DC边上的点,且AE=CF,
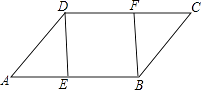
(1)求证:△ADE≌△CBF.
(2)若∠DEB=90°,求证:四边形DEBF是矩形.
相关试题

