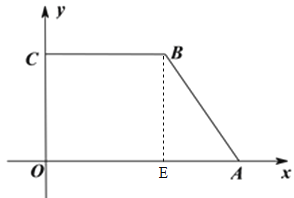
【题目】如图,在平面直角坐标系中,点A、C分别在x轴上、y轴上,CB//OA,OA=8,若点B的坐标为(a,b),且b=![]() .
.
(1)直接写出点A、B、C的坐标;
(2)若动点P从原点O出发沿x轴以每秒2个单位长度的速度向右运动,当直线PC把四边形OABC分成面积相等的两部分停止运动,求P点运动时间;
(3)在(2)的条件下,在y轴上是否存在一点Q,连接PQ,使三角形CPQ的面积与四边形OABC的面积相等?若存在,求点Q的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)A(8,0),B(4,4),C(0.4);(2)t=![]() ;(3)
;(3)![]() (0,13),
(0,13),![]() (0,-5)
(0,-5)
【解析】分析:(1)根据线段的长和线段的特点以及二次根式有意义的条件确定出点的坐标;
(2)先求出S四边形OABC=24,从而得到![]() ×OP×4=12,求出OP即可得到结论;
×OP×4=12,求出OP即可得到结论;
(3)根据四边形OABC的面积求出△CPQ的面积是24,即可求出点Q的坐标.
详解:(1)过B作BE⊥OA于E.∵a-4≥0且4-a≥0,∴a=4,∴b=4,∴B(4,4),∴OC=EB=4,∴C(0.4).∵OA=8,∴A(8,0);
(2)设运动时间t秒,∴OP=2t, ∴![]() 2t
2t![]() 4=
4=![]() ,∴t=3.
,∴t=3.
(3)设Q(0,y), ∵![]() ,∴
,∴![]()
![]()
![]() =
=![]() (4+8)
(4+8)![]() 4,
4,
∴![]() =13,
=13,![]() =-5,∴
=-5,∴![]() (0,13),
(0,13),![]() (0,-5)
(0,-5)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DE、FG相交于点H.

(1)判断线段DE、FG的位置关系,并说明理由;
(2)连结CG,求证:四边形CBEG是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】己知:如图,E、F分别是ABCD的AD、BC边上的点,且AE=CF.
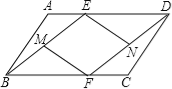
(1)求证:△ABE≌△CDF;
(2)若M、N分别是BE、DF的中点,连接MF、EN,试判断四边形MFNE是怎样的四边形,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明的妈妈在菜市场买回3斤萝卜、2斤排骨,准备做萝卜排骨汤.
妈妈:“今天买这两样菜共花了45元,上月买同重量的这两样菜只要36元”;
爸爸:“报纸上说了萝卜的单价上涨50%,排骨单价上涨20%”;
小明:“爸爸、妈妈,我想知道今天买的萝卜和排骨的单价分别是多少?”
请你通过列方程(组)求解这天萝卜、排骨的单价(单位:元/斤).
-
科目: 来源: 题型:
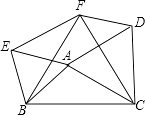
查看答案和解析>>【题目】如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF,则下列结论::①△EBF≌△DFC;②四边形AEFD为平行四边形;③当AB=AC,∠BAC=120°时,四边形AEFD是正方形.其中正确的结论是 . (请写出正确结论的序号).
-
科目: 来源: 题型:
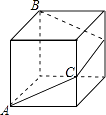
查看答案和解析>>【题目】如图,一只蚂蚁沿着棱长为2的正方体表面从点A出发,经过3个面爬到点,如运动的路径是最短的,则AC的长为
-
科目: 来源: 题型:
查看答案和解析>>【题目】亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某市初中学生每天进行体育锻炼的时间情况,随机抽样调查了100名涌中学生,根据调查结果得到如图所示的统计图表.
类别
时间t(小时)
人数
A
t≤0.5
5
B
0.5<t≤1
20
C
1<t≤1.5
a
D
1.5<t≤2
30
E
t>2
10
请根据图表信息解答下列问题:
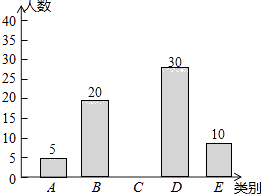
(1)a=;
(2)补全条形统计图;
(3)据了解该市大约有30万名初中学生,请估计该市初中学生每天进行体育锻炼时间在1小时以上的人数.
相关试题

